ЬтФПФкШн
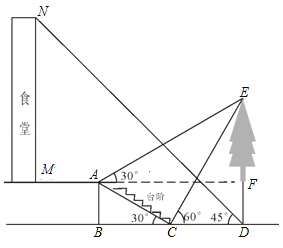
ЁОЬтФПЁПЃЈ2017КўББЪЁЖѕжнЪаЃЉаЁУїЯывЊВтСПбЇаЃЪГЬУКЭЪГЬУе§ЧАЗНвЛПУЪїЕФИпЖШЃЌЫћДгЪГЬУТЅЕзMДІГіЗЂЃЌЯђЧАзп3УзЕНДяAДІЃЌВтЕУЪїЖЅЖЫEЕФбіНЧЮЊ30ЁуЃЌЫћгжМЬајзпЯТЬЈНзЕНДяCДІЃЌВтЕУЪїЕФЖЅЖЫEЕФбіНЧЪЧ60ЁуЃЌдйМЬајЯђЧАзпЕНДѓЪїЕзDДІЃЌВтЕУЪГЬУТЅЖЅNЕФбіНЧЮЊ45ЁуЃЎвбжЊAЕуРыЕиУцЕФИпЖШAB=2УзЃЌЁЯBCA=30ЁуЃЌЧвBЁЂCЁЂDШ§ЕудкЭЌвЛжБЯпЩЯЃЎ
ЃЈ1ЃЉЧѓЪїDEЕФИпЖШЃЛ
ЃЈ2ЃЉЧѓЪГЬУMNЕФИпЖШЃЎ
ЁОД№АИЁПЃЈ1ЃЉ6ЃЛЃЈ2ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЃЈ1ЃЉЩшDE=xЃЌПЩЕУEF=DEЉDF=xЉ2ЃЌДгЖјЕУAF=![]() ЃЈxЉ2ЃЉЃЌдйЧѓГіCD=
ЃЈxЉ2ЃЉЃЌдйЧѓГіCD=![]() xЁЂBCЕФГЄЃЌИљОнAF=BDПЩЕУЙигкxЕФЗНГЬЃЌНтжЎПЩЕУЃЛ
xЁЂBCЕФГЄЃЌИљОнAF=BDПЩЕУЙигкxЕФЗНГЬЃЌНтжЎПЩЕУЃЛ
ЃЈ2ЃЉбгГЄNMНЛDBбгГЄЯпгкЕуPЃЌжЊAM=BP=3ЃЌгЩЃЈ1ЃЉЕУCD=![]() x=
x=![]() ЁЂBC=
ЁЂBC=![]() ЃЌИљОнNP=PDЧвAB=MPПЩЕУД№АИЃЎ
ЃЌИљОнNP=PDЧвAB=MPПЩЕУД№АИЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉШчЭМЃЌЩшDE=xЃЌЁпAB=DF=2ЃЌЁрEF=DEЉDF=xЉ2ЃЌЁпЁЯEAF=30ЁуЃЌЁрAF=![]() =
=![]() ЃЌгжЁпCD=
ЃЌгжЁпCD=![]() =
=![]() =
=![]() xЃЌBC=
xЃЌBC=![]() =
=![]() =
=![]() ЃЌЁрBD=BC+CD=
ЃЌЁрBD=BC+CD=![]() +
+![]() xЃЌгЩAF=BDПЩЕУ
xЃЌгЩAF=BDПЩЕУ![]() ЃЈxЉ2ЃЉ=
ЃЈxЉ2ЃЉ=![]() +
+![]() xЃЌНтЕУЃКx=6ЃЌЁрЪїDEЕФИпЖШЮЊ6УзЃЛ
xЃЌНтЕУЃКx=6ЃЌЁрЪїDEЕФИпЖШЮЊ6УзЃЛ
ЃЈ2ЃЉбгГЄNMНЛDBбгГЄЯпгкЕуPЃЌдђAM=BP=3ЃЌгЩЃЈ1ЃЉжЊCD=![]() x=
x=![]() ЁС6=
ЁС6=![]() ЃЌBC=
ЃЌBC=![]() ЃЌЁрPD=BP+BC+CD=3+
ЃЌЁрPD=BP+BC+CD=3+![]() +
+![]() =3+
=3+![]() ЃЌЁпЁЯNDP=45ЁуЃЌЧвMP=AB=2ЃЌЁрNP=PD=3+
ЃЌЁпЁЯNDP=45ЁуЃЌЧвMP=AB=2ЃЌЁрNP=PD=3+![]() ЃЌЁрNM=NPЉMP=3+
ЃЌЁрNM=NPЉMP=3+![]() Љ2=
Љ2=![]() ЃЌЁрЪГЬУMNЕФИпЖШЮЊ
ЃЌЁрЪГЬУMNЕФИпЖШЮЊ![]() УзЃЎ
УзЃЎ
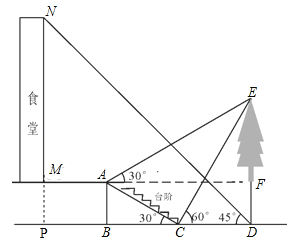

 ЭЌВНСЗЯАЧПЛЏЭиеЙЯЕСаД№АИ
ЭЌВНСЗЯАЧПЛЏЭиеЙЯЕСаД№АИ