题目内容
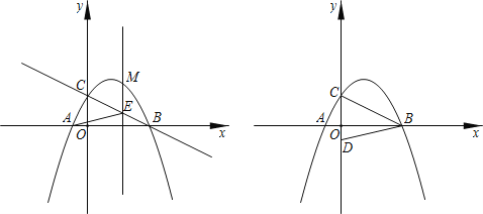
【题目】如图,在平面直接坐标系中,将反比例函数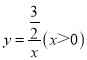 的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点
的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点![]() ,
,![]()
![]() 的直线与曲线l相交于点C、D,则sin∠COD=___ .
的直线与曲线l相交于点C、D,则sin∠COD=___ .
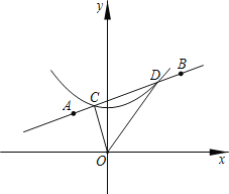
【答案】![]() .
.
【解析】
由题![]() ,
,![]() ,可得OA⊥OB,建立如图新的坐标系,OB为x′轴,OA为y′轴,利用方程组求出C、D的坐标,根据勾股定理求得OC、OD的长,根据S△OCD=S△OBC-S△OBD计算求得△OCD的面积,根据三角形面积公式求得CE的长,然后解直角三角形即可求得sin∠COD的值.
,可得OA⊥OB,建立如图新的坐标系,OB为x′轴,OA为y′轴,利用方程组求出C、D的坐标,根据勾股定理求得OC、OD的长,根据S△OCD=S△OBC-S△OBD计算求得△OCD的面积,根据三角形面积公式求得CE的长,然后解直角三角形即可求得sin∠COD的值.
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴OA⊥OB,
建立如图新的坐标系,OB为x′轴,OA为y′轴.
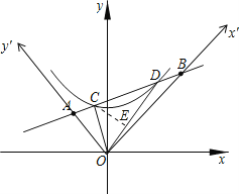
在新的坐标系中,A(0,2),B(4,0),
∴直线AB解析式为y′=-![]() x′+2,
x′+2,
由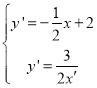 ,解得
,解得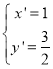 或
或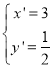 ,
,
∴C(1,![]() ),D(3,
),D(3,![]() ),
),
∴S△OCD=S△OBC-S△OBD=![]() ,
,
∵C(1,![]() ),D(3,
),D(3,![]() ),
),
∴OC=![]() =
=![]() ,OD=
,OD=![]() =
=![]() ,
,
作CE⊥OD于E,
∵S△OCD=![]() ODCE=2,
ODCE=2,
∴CE=![]() ,
,
∴sin∠COD=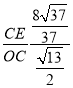 =
=![]() ,
,
故答案为![]() .
.

练习册系列答案
相关题目
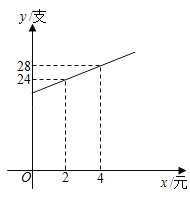
【题目】小李经营的车饰店销售某品牌车漆修复液,已知其进价为40元/支,试销阶段发现将售价定为80元/支时,每天可销售20支,后来为了扩大销售量,小李适当降低了售价,销售量y(支)与降价x(元)的关系如图所示.
(1)请仔细读题,并补全下面表格:
降价x/元 | … | 2 | 4 |
| x | … |
销量y/支 | … | 24 | 28 | 30 |
| … |
(2)若要使得平均每天销售这种修复液的利润W最大,则每支修复液应该降价多少元?最大的利润W为多少元?