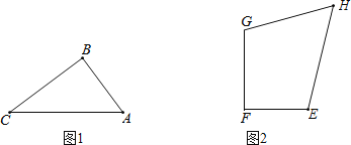Question

【题目】如图，在Rt△ABC中，∠C=90°，AC=4，cosA=，点D是斜边AB上的动点且不与A，B重合，连接CD，点B'与点B关于直线CD对称，连接B'D，当B'D垂直于Rt△ABC的直角边时，BD的长为______．

Answer 1

【答案】1或3．

【解析】

由cosA=，AC=4，得AB=5，从而得BC=3，分两种情况：①如图1中，当B′D⊥BC时，②如图2中，当DB′⊥AC于E时，分别求出BD的值，即可．

∵cosA==，AC=4，

∴AB=5，

∴BC===3，

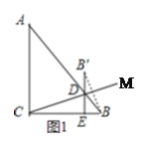
①如图1中，当B′D⊥BC时，设B′D交BC于E，

∵点B'与点B关于直线CD对称，

∴∠ADC=∠BDM=∠B′DM=∠CDE，

∵∠ACB=∠B′EB=90°，

∴AC∥B′E，

∴∠ACD=∠CDE=∠ADC，

∴AD=AC=4，

∴BD=AB-AD=5-4=1；

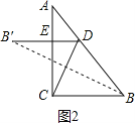
②如图2，当DB′⊥AC于E时，同理可得：BC=BD=3，

综上所述，满足条件的BD的值为1或3．

故答案是：1或3．