题目内容
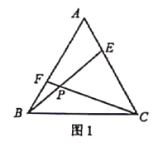
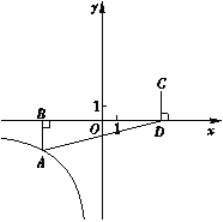
【题目】如图,AB是⊙O的直径,C是圆上一点,弦CD⊥AB于点E,且DC=AD.过点A作⊙O的切线,过点C作DA的平行线,两直线交于点F,FC的延长线交AB的延长线于点G.
(1)求证:FG与⊙O相切;
(2)连接EF,求![]() 的值.
的值.

【答案】(1)见解析;(2)![]()
【解析】(1)连接OC、AC,先证DC=AD= AC,得出△ACD为等边三角形,所以∠D =∠DCA=∠DAC =60°,从而FG∥DA,易知![]() , 得出FG⊥OC ,则FG与⊙O相切;(2)作EH⊥FG于点H.设CE= a,则DE= a,AD=2a,易证四边形AFCD为平行四边形,因为DC =AD,AD=2a,所以 四边形AFCD为菱形,由(1)得∠DCG=60°,从而可求出EH、CH的值,然后可知FH的长度,利用锐角三角函数的定义即可求出tan∠EFC的值.
, 得出FG⊥OC ,则FG与⊙O相切;(2)作EH⊥FG于点H.设CE= a,则DE= a,AD=2a,易证四边形AFCD为平行四边形,因为DC =AD,AD=2a,所以 四边形AFCD为菱形,由(1)得∠DCG=60°,从而可求出EH、CH的值,然后可知FH的长度,利用锐角三角函数的定义即可求出tan∠EFC的值.
(1)证明:如图,连接OC,AC.

∵ AB是⊙O的直径,弦CD⊥AB于点E,
∴ CE=DE,AD=AC.
∵ DC=AD,
∴ DC=AD= AC.
∴ △ACD为等边三角形.
∴ ∠D =∠DCA=∠DAC =60°.
∴ ![]() .
.
∵ FG∥DA,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴ FG⊥OC.
∴ FG与⊙O相切.
(2)解:如图,作EH⊥FG于点H.
设CE= a,则DE= a,AD=2a.
∵ AF与⊙O相切,
∴ AF⊥AG.
又∵ DC⊥AG,
可得AF∥DC.
又∵ FG∥DA,
∴ 四边形AFCD为平行四边形.
∵ DC =AD,AD=2a,
∴ 四边形AFCD为菱形.
∴ AF=FC=AD=2 a,∠AFC=∠D = 60°.
由(1)得∠DCG= 60°,![]() ,
,![]() .
.
∴ ![]() .
.
∵ 在Rt△EFH中,∠EHF= 90°,
∴ 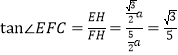 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在一个不透明的盒子中装有a个除颜色外完全相同的红球和白球,其中红球有b个,将盒中的球摇匀后从中任意摸出1个球,记录颜色后将球放回盒中,重复进行这过程,如表记录了某班一次摸球实验情况:
摸球总数n | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
摸到红球数m | 325 | 1336 | 3203 | 6335 | 8073 | 12628 |
摸到红球的频率(精确到0.001) | 0.813 | 0.891 | 0.915 | 0.905 | 0.897 | 0.902 |
(1)由此估计任意摸出1个球为红球的概率约是 (精确到0.1)
(2)实验结束后,小明发现了一个一般性的结论:盒子中共有a个球,其中红球有b个,则摇匀后从中任意摸出1个球为红球的概率P可以表示为![]() ,这个结论也得到了老师的证实根据小明的发现,若在该盒子中再放入除颜色外与原来的球完全相同的2个红球和2个白球,摇匀后从中任意摸出1个球为红球的概率为P’,请通过计算比较P与P'的大小.
,这个结论也得到了老师的证实根据小明的发现,若在该盒子中再放入除颜色外与原来的球完全相同的2个红球和2个白球,摇匀后从中任意摸出1个球为红球的概率为P’,请通过计算比较P与P'的大小.