题目内容
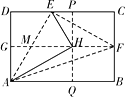
【题目】如图1，平面直角坐标系中，直线y=kx+b与x轴交于点A（6，0），与y轴交于点B，与直线y=2x交于点C（a，4）．
（1）求点C的坐标及直线AB的表达式；
（2）如图2，在（1）的条件下，过点E作直线l⊥x轴于点E，交直线y=2x于点F，交直线y=kx+b于点G，若点E的坐标是（4，0）．
①求△CGF的面积；
②直线l上是否存在点P，使OP+BP的值最小？若存在，直接写出点P的坐标；若不存在，说明理由；
（3）若（2）中的点E是x轴上的一个动点，点E的横坐标为m（m＞0），当点E在x轴上运动时，探究下列问题：
当m取何值时，直线l上存在点Q，使得以A，C，Q为顶点的三角形与△AOC全等？请直接写出相应的m的值．
【答案】（1）y=﹣x+6；（2）①6；②P（4，3）；（3）A题：m的值为2或6或8．B题：m的值为3或6或
或
．
【解析】
（1）将C（2，4）和A（6，0）代入y=kx+b，即可得到直线AB的解析式；
（2）①设点F（4，y1），G（4，y2），分别代入y=2x和y=-x+6，可得FE=8，GE=2，FG=6，过点C作CH⊥FG于H，依据S△FCG=
FG×CH，进行计算即可；②设点O关于直线l的对称点为D（8，0），设直线BD的解析式为y=mx+n，将B（0，6），D（8，0）代入y=mx+n，可得直线BD的解析式为y=-
x+6，令x=4，则y=3，即可得出P（4，3）；
（3）选A题时，需要分数轴情况进行讨论，画出图形，依据全等三角形的对应顶点的位置，即可得到m的值；选B题时，依据△BFG是等腰三角形分四种情况进行讨论，进而得出m的值．
（1）将点C（a，4）代入y=2x，可得a=2，
∴C（2，4），
将C（2，4）和A（6，0）代入y=kx+b，可得
，解得
，
∴直线AB的解析式为y=﹣x+6；
（2）①如图1，∵l⊥x轴，点E，F，G都在直线l上，且点E的坐标为（4，0），
∴点F，G的横坐标均为4，
设点F（4，y1），G（4，y2），分别代入y=2x和y=﹣x+6，可得
y1=8，y2=2，
∴F（4，8），G（4，2），
∴FE=8，GE=2，FG=6，
如图2，过点C作CH⊥FG于H，
∵C（2，4），
∴CH=4﹣2=2，
∴S△FCG=FG×CH=×6×2=6；
②存在点P（4，3），使得BP+OP的值最小．
理由：设点O关于直线l的对称点为D（8，0），
设直线BD的解析式为y=mx+n，
将B（0，6），D（8，0）代入y=mx+n，可得
，解得
，
∴直线BD的解析式为y=﹣x+6，
点P在直线l：x=4上，令x=4，则y=3，
∴P（4，3）；
（3）A题：m的值为2或6或8．
理由：分三种情况讨论：
①当△OAC≌△QCA，点Q在第四象限时，∠ECA=∠EAC，
∴AE=CE=4，OE=6﹣4=2，
∴m=2；
②当△ACO≌△ACQ，Q在第一象限时，OE=AO=6，
∴m=6；
③当△ACO≌△CAQ，点Q在第四象限时，四边形AOCQ是平行四边形，CQ=AO=6，AE=2，
∴OE=8，
∴m=8；
B题：m的值为3或6或
或
．
理由：分四种情况讨论：
①如图，当BG=GF时，
m=﹣m+6﹣2m，
解得m=；
②如图，当BF=GF时，m=2m﹣（﹣m+6），
解得m=3；
③如图，当GB=GF时，m=2m﹣（﹣m+6），
解得m=；
④如图，当BG=BF时，FG=BG，即2m﹣（﹣m+6）=×m，
解得m=6．
