题目内容
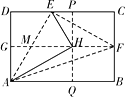
【题目】如图,矩形纸片ABCD中,G、F分别为AD、BC的中点,将纸片折叠,使D点落在GF上,得到△HAE , 再过H点折叠纸片,使B点落在直线AB上,折痕为PQ.连接AF、EF , 已知HE=HF.下列结论:①△MEH为等边三角形;②AE⊥EF;③△PHE∽△HAE;④![]() ,
, 
其中正确的结论是
A.①②③
B.①②④
C.①③④
D.①②③④
【答案】D
【解析】解:①由折叠易得AH=AD,∠DAE=HAE,
∠AHE=∠D=90°,PQ=BC=AD,PQ⊥AB,
因为G,F分别为AD、BC的中点,
所以H也是PQ的中点,
则在Rt△AHQ中,AH=2HQ,则∠HAQ=30°,
所以∠DAE=HAE=∠HAQ=30°,
则∠AEH=60°,∠AHM=∠HAQ=30°,
所以∠EMH=∠AEH=60°,
则△MEH为等边三角形,故①正确;
②由①得MH=EH=HF,则△MEF为直角三角形,即AE⊥EF , 故②正确;
③在Rt△AHE中,![]() =sin30°=
=sin30°=![]() ,
,
同理,在Rt△AHQ中,![]() =sin30°=
=sin30°=![]() ,
,
则![]() =
=![]() =
=![]() ,
,
又∠AHE=∠HPE=90°,
∴△PHE∽△HAE , 故③正确;
④设AD=x,则AH=x,BQ=HF=HE=![]() x,AQ=
x,AQ=![]() AH=
AH=![]() x,
x,
则AB=AQ+BQ=![]() x,
x,
所以![]() =
=![]() =
=![]() ,
,
故④正确.
故选 D.
【考点精析】本题主要考查了矩形的性质的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目