题目内容
【题目】如图,正方形ABCD中,内部有6个全等的正方形,小正方形的顶点E、F、G、H分
别在边AD、AB、BC、CD上,则tan∠DEH=( )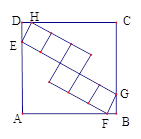
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】∵正方形ABCD的边长为10a,
∴∠A=∠B=90° ,AB=10a,
过点G作GP⊥ AD,垂足为P,则∠DPG=∠APG.
∴四边形APGB是矩形,
∴∠PGF+∠BGF=90°,PG=AB=10a,
∵六个大小完全一样的小正方形如图放置在大正方形中,
∴∠EGP+∠PGF=90°,
∴∠EGP=∠BGF
∴△BGF∽△PGE,
∴![]() ,
,
∴GB=AP=2a,
同理DE=2a,
∴PE=AD-AP-DE=6a,
∴EG=![]() =2
=2![]() a,
a,
∴小正方形的边长为![]() a,
a,
∴DH=![]() =
=![]() a
a
∴tan∠DEH=![]() =
=![]()
故本题正确选项为A。
【考点精析】根据题目的已知条件,利用勾股定理的概念和相似三角形的性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;对应角相等,对应边成比例的两个三角形叫做相似三角形.

【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如表所示
国外品牌 | 国内品牌 | |
进价(万元/部) | 0.44 | 0.2 |
售价(万元/部) | 0.5 | 0.25 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润