题目内容
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD以点D为中心逆时针旋转90°至ED,连结AE,CE,则△ADE的面积是( ) 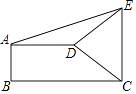
A.1
B.2
C.3
D.4
【答案】A
【解析】解:作DH⊥BC于H,EF⊥AD于F,如图,则四边形ABHD为矩形,
∴BH=AD=2,
∴CH=BC﹣BH=3﹣2=1,
∵腰CD以点D为中心逆时针旋转90°至ED,
∴DE=DC,∠EDC=90°,
∵∠EDF+∠CDF=90°,∠CDF+∠CDH=90°,
∴∠EDF=∠HDC,
在△EDF和△CDH中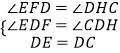 ,
,
∴△EDF≌△CDH,
∴EF=CH=1,
∴△ADE的面积= ![]() ×2×1=1.
×2×1=1.
故选A.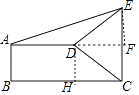
【考点精析】解答此题的关键在于理解直角梯形的相关知识,掌握一腰垂直于底的梯形是直角梯形,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如表所示
国外品牌 | 国内品牌 | |
进价(万元/部) | 0.44 | 0.2 |
售价(万元/部) | 0.5 | 0.25 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润
【题目】七(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用 水量x/m3 | 0< x≤5 | 5< x≤10 | 10< x≤15 | 15< x≤20 | x>20 |
频数/户数 | 12 | 20 | 3 | ||
百分比 | 12% | 7% |
若该小区有800户家庭,据此估计该小区月均用水量不超过10 m3的家庭有________户.