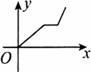
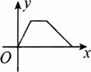
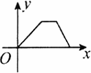
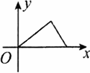
题目内容
| |||||
答案:
解析:
解析:
|
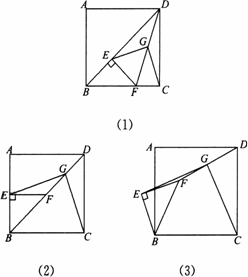
(1)证明:在Rt△FCD中, ∵G为斜边DF的中点, ∴ 在Rt△DEF中, ∵G为斜边DF的中点, ∴ ∴CG=EG. (2)解:(1)中结论仍然成立,即EG=CG. 连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点. 在△DAG与△DCG中, ∵AD=CD,∠ADG=∠CDG=45°,DG=DG, ∴△DAG≌DCG. ∴AG=CG. 在△DMG与△FNG中, ∵∠DGM=∠FCN,FG=DG,∠MDG=∠NFG=45°, ∴△DMG≌△FNG.∴MG=NG. 在矩形AENM中,AM=EN. 在Rt△AMG与Rt△ENG中, ∵AM=EN,MG=NG, ∴△AMG≌△ENG. ∴AG=EG. ∴EG=CG. (3)解:(1)中的结论仍然成立, 即EG=CG.其他的结论还有:EG⊥CG. |

练习册系列答案
相关题目