题目内容
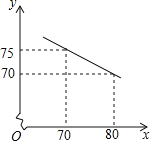
【题目】某商店经销一种销售成本为每千克40元的水产品,规定试销期间销售单价不低于成本价.据试销发现,月销量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() .若该商店获得的月销售利润为
.若该商店获得的月销售利润为![]() 元,请回答下列问题:
元,请回答下列问题:
(1)请写出月销售利润![]() 与销售单价
与销售单价![]() 之间的关系式(关系式化为一般式);
之间的关系式(关系式化为一般式);
(2)在使顾客获得实惠的条件下,要使月销售利润达到8000元,销售单价应定为多少元?
(3)若获利不高于![]() ,那么销售单价定为多少元时,月销售利润达到最大?
,那么销售单价定为多少元时,月销售利润达到最大?
【答案】(1)W=﹣10x2+1400x﹣40000;(2)销售单价应定为60元;(3)销售单价定为68元时,月销售利润达到最大.
【解析】
(1)根据总利润=每千克的利润×月销量,即可求出月销售利润![]() 与销售单价
与销售单价![]() 之间的关系式,然后化为一般式即可;
之间的关系式,然后化为一般式即可;
(2)将![]() =800代入(1)的关系式中,求出x即可;
=800代入(1)的关系式中,求出x即可;
(3)根据获利不高于![]() ,即可求出x的取值范围,然后根据二次函数的增减性,即可求出当月销售利润达到最大时,销售单价的定价.
,即可求出x的取值范围,然后根据二次函数的增减性,即可求出当月销售利润达到最大时,销售单价的定价.
解:(1)根据题意得,W=(x﹣40)(﹣10x+1000)
=﹣10x2+1000x+400x﹣40000
=﹣10x2+1400x﹣40000;
(2)当W=﹣10x2+1400x﹣40000=8000时,
得到x2﹣140x+4800=0,
解得:x1=60,x2=80,
∵使顾客获得实惠,
∴x=60.
答:销售单价应定为60元.
(3)W=-10x2+1400x﹣40000
=-10(x﹣70)2+9000
∵获利不得高于70%,即x﹣40≤40×70%,
∴x≤68.
∵-10<0,对称轴为直线x=70
∴当x≤68时,y随x的增大而增大
∴当x=68时,W最大=8960.
答:销售单价定为68元时,月销售利润达到最大.

练习册系列答案
相关题目