Question

【题目】如图，边长为4的正六边形ABCDEF的中心与坐标原点O重合，AF∥x轴，将该正六边形绕原点O顺时针旋转n次，每次旋转60°，当n=63时，顶点F的坐标为_____．

Answer 1

【答案】（﹣2，）

【解析】

连接OA、OC、OD、OF，作FH⊥OE于H，根据正六边形的性质得到∠AOF=∠FOE=∠EOD=∠DOC=∠COB=∠BOA=60°，根据旋转变换的性质、直角三角形的性质计算．

连接OA、OC、OD、OF，作FH⊥OE于H，

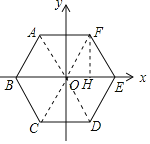
∵六边形ABCDEF是正六边形，

∴∠AOF=∠FOE=∠EOD=∠DOC=∠COB=∠BOA=60°，

∵将正六边形ABCDEF绕原点O顺时针旋转，每次旋转60°，

∴点A旋转6次回到点A，

63÷6=10…3，

∴正六边形ABCDEF绕原点O顺时针旋转63次，与点D重合，

∵∠AOF=60°，OA=OF，

∴△AOF是等边三角形，

∴OF=4，又∠FOE=60°，

∴OH=2，FH=2，

∴顶点F的坐标为（-2，-2），

故答案为：（-2，-2），