题目内容
【题目】如图，禁止捕鱼期间，某海上稽查队在某海域巡逻，上午某一时刻在A处接到指挥部通知，在他们东北方向距离12海里的B处有一艘捕鱼船，正在沿南偏东75°方向以每小时10海里的速度航行，稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发，在C处成功拦截捕鱼船，求巡逻船从出发到成功拦截捕鱼船所用的时间．
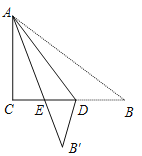
【答案】解：设巡逻船从出发到成功拦截所用时间为x小时；如图所示，
由题意得：∠ABC=45°+75°=120°，AB=12，BC=10x，AC=14x，
过点A作AD⊥CB的延长线于点D，
在Rt△ABD中，AB=12，∠ABD=45°+（90°﹣75°）=60°，
∴BD=ABcos60°= 
AB=6，AD=ABsin60°=6 
，
∴CD=10x+6．
在Rt△ACD中，由勾股定理得： 
，
解得： 
（不合题意舍去）．
答：巡逻船从出发到成功拦截所用时间为2小时．
【解析】根据题意，添加辅助线过点A作AD⊥CB的延长线于点D，易求得∠ABC的度数，在Rt△ABD中，由解直角三角形求出BD，AD的长度，表示出CD的长，在Rt△ACD中，由勾股定理列出方程求解即可。
【考点精析】本题主要考查了勾股定理的概念和解直角三角形的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能正确解答此题．
练习册系列答案
相关题目
