题目内容
【题目】如图,正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点M.求证:AE⊥BF.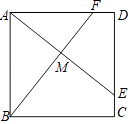
【答案】证明:∵四边形ABCD是正方形,
∴∠BAD=∠ADE=90°,AD=AB=DC,
∵DF=CE,
∴AF=DE,
∵在△ABF和△DAE中,
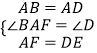 ,
,
∴△ABF≌△DAE(SAS);
∴∠AFB=∠DEA,
∵∠D=90°,
∴∠DEA+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AMF=180°﹣90°=90°,
∴AE⊥BF.
【解析】因为四边形ABCD是正方形,得到四个角都是直角,四条边都相等,从而得到△ABF≌△DAE,得到对应角相等,得到∠AMF=90°.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
【题目】下表是加热食用油的温度变化情况:
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现,烧了110![]() 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )
A.没有加热时,油的温度是10℃B.加热50![]() ,油的温度是110℃
,油的温度是110℃
C.估计这种食用油的沸点温度约是230℃D.每加热10![]() ,油的温度升高30℃
,油的温度升高30℃