题目内容
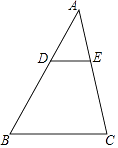
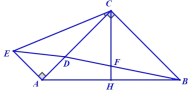
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CH为△ABC斜边上的中线,点F为CH上一点,连接BF并延长交AC于点D,过点A作AE⊥AC,连接CE和DE,若∠ACE=2∠ABF,CE=13,CD=8,则△CDE的面积为__________.
【答案】20
【解析】
延长BD交CE于G点,作![]() 交CE于K,交GD于O,设
交CE于K,交GD于O,设![]() ,则
,则![]() ,根据
,根据![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,可证
,可证![]() ,则
,则![]() ,根据ASA易证明
,根据ASA易证明![]() ,利用
,利用![]() ,
,![]() ,可证
,可证![]() ,可得
,可得![]() ,再利用三角形的面积公式即可求解.
,再利用三角形的面积公式即可求解.
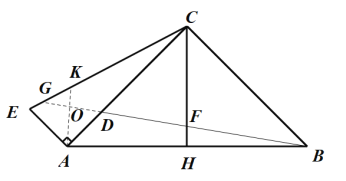
解:如图示:延长BD交CE于G点,作![]() 交CE于K,交GD于O,
交CE于K,交GD于O,
设![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]()
∴![]() ,
,
∴![]()
∴![]()
在Rt△ADO和Rt△BDC中,
![]() ,
,![]() ,
,
∴![]() ,则有
,则有![]()
在△CAK和△CGD中,
![]() ,
,![]() ,
,![]()
∴![]()
∴![]() ,
,![]()
∴![]()
又∵![]()
即有![]() ,
,
∴![]()
∴![]() ,
,
故答案为:20.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】下表是加热食用油的温度变化情况:
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现,烧了110![]() 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )
A.没有加热时,油的温度是10℃B.加热50![]() ,油的温度是110℃
,油的温度是110℃
C.估计这种食用油的沸点温度约是230℃D.每加热10![]() ,油的温度升高30℃
,油的温度升高30℃