题目内容
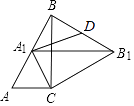
【题目】如图,ABCD的对角线AC,BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)连接DE,BF,若BD⊥EF,试探究四边形EBFD的形状,并对结论给予证明.

【答案】(1)详见解析;(2)四边形EBFD为菱形.
【解析】
(1)根据平行四边形的性质可得BO=DO,AO=CO,再利用等式的性质可得EO=FO,然后再利用SAS定理判定△BOE≌△DOF即可;
(2)根据BO=DO,FO=EO可得四边形BEDF是平行四边形,再根据对角线互相垂直的平行四边形是菱形可得四边形EBDF为菱形.
(1)证明:∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO.
∵AE=CF,
∴AO-AE=CO-CF,
即EO=FO.
在△BOE和△DOF中,
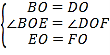
∴△BOE≌△DOF(SAS).
(2)四边形EBFD为菱形,
证明:∵BO=DO,FO=EO,
∴四边形BEDF是平行四边形.
∵BD⊥EF,
∴四边形EBFD为菱形.

练习册系列答案
相关题目
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |

(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.