��Ŀ����
����Ŀ��ij��ѧΪ��������У���ƻ������ס������ֹ����������¹�����ͼ�飬���鷢�֣�������һ���������ȹ���һ����������60Ԫ��������������1�����������2���������ʽ�660Ԫ��
��1���ס����������ÿ���ļ۸�ֱ��Ƕ���Ԫ��
��2������У�ƻ����������ֹ������20�������������������������ڼ�������������ѧУ�����ܹ��ṩ�ʽ�4320Ԫ������ѧУ���ļ��ֹ�����
���𰸡���1���������ÿ���ļ۸�Ϊ180Ԫ���������ÿ���ļ۸�Ϊ240Ԫ����2��ѧУ�Ĺ������������֣�����һ���������8�����������12�������������������9�����������11�������������������10�����������10����
��������
��1����������ÿ���ļ۸�ΪxԪ���������ÿ���ļ۸�ΪyԪ��������������һ���������ȹ���һ����������60Ԫ��������������1�����������2���������ʽ�660Ԫ�������ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2���蹺��������m���������������20-m���������������������������ڼ�������������ѧУ�����ܹ��ṩ�ʽ�4320Ԫ�����ɵó�����m��һԪһ�β���ʽ�飬��֮���ɵó�m��ȡֵ��Χ���ٽ��mΪ�������ɵó���������
��1����������ÿ���ļ۸�ΪxԪ���������ÿ���ļ۸�ΪyԪ��
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
�𣺼������ÿ���ļ۸�Ϊ180Ԫ���������ÿ���ļ۸�Ϊ240Ԫ��
��2���蹺��������m���������������20-m������
�����⣬�ã�
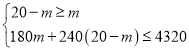 ��
��
��ã�8��m��10��
��m������
��m����ȡ��ֵΪ��8��9��10��
��ѧУ�Ĺ������������֣�
����һ���������8�����������12����
���������������9�����������11����
���������������10�����������10����

 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�����Ŀ��Ϊ�˴��������������У���Ҫ����ס����������͵ķ�������Ͱ�滻ԭ��������Ͱ��![]() ��
��![]() ��
��![]() ����С����������������ܼ������ʾ��
����С����������������ܼ������ʾ��
��������Ͱ�������ף� | ��������Ͱ�������ף� | �ܼۣ�Ԫ�� | |
|
|
|
|
|
|
|
|
|
|
|
|
��1���ʼ�������Ͱ����������Ͱ�ĵ��۷ֱ���ÿ����Ԫ��
��2����![]() ��
��![]() ��ֵ��
��ֵ��