Question

【题目】如图，AB是△ABC外接圆⊙O的直径，D是AB延长线上一点，且BD= AB，∠A=30°，CE⊥AB于E，过C的直径交⊙O于点F，连接CD、BF、EF．

（1）求证：CD是⊙O的切线；
（2）求：tan∠BFE的值．

Answer 1

【答案】
（1）证明：∵AB是⊙O的直径，

∴∠ACB=90°，

∵∠A=30°，

∴BC= ，

∵OB= ，BD= ，

∴BC=OB=BD，

∴BC= ，

∴OC⊥CD，

∵OC是半径，

∴CD是⊙O的切线；

（2）解：过点E作EH⊥BF于H，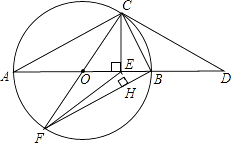

设EH=a，

∵CF是⊙O直径，

∴∠CBF=90°=∠ACB，

∴∠CBF+∠ACB=180°，

∴AC∥BF，

∴∠ABF=∠A=30°，

∴BH= EH=a ，BE=2EH=2a，

∵CE⊥AB于E，

∴∠A+∠ABC=90°=∠ECB+∠ABC，

∴∠ECB=∠A=30°，

∴BC=2BE=4a，

∵∠BFC=∠A=30°，∠CBF=90°，

∴BF= =4a ，

∴FH=BF﹣BH=4a ﹣a =3a ，

∴tan∠BFE= = = ．

【解析】（1）根据已知条件证得OC⊥CD，再有切线的判定即可得到CD是⊙O的切线；
（2）过点E作EH⊥BF于H，设EH=a，利用角之间的关系可得到AC∥BF，从而得到BH和BE的长，进而可得到BF的长，此时可求得FH的长，即可求得所求结答案．