题目内容
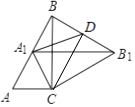
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得△A1B1C1 , 且点A1落在边AB边上,取BB1的中点D,连接CD,则CD的长为( )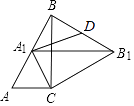
A.![]()
B.![]()
C.2
D.3
【答案】A
【解析】解:∵∠C=90°,∠A=60°,AC=1,
∴∠ABC=30°,
∴AB=2,BC= ![]() AC=
AC= ![]() ,
,
由旋转的性质可知,CA=CA′,由∠A=60°,
∴△ACA′是等边三角形,
∴AA′=1,
∴A′B=1,
由旋转的性质可知,△B1BC是等边三角形,
∴BB1=BC= ![]() ,
,
∵BB1的中点是D,
∴CD⊥BB1,BD= ![]() BB1=
BB1= ![]() ,
,
∴CD= ![]() BD=
BD= ![]() ,
,
所以答案是:A.
【考点精析】本题主要考查了等腰三角形的性质和含30度角的直角三角形的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能正确解答此题.

【题目】为迎接济川中学红歌演讲比赛,济川校区七年级(15)(16)班决定订购同一套服装,两班一共有103人(15班人数多于16班),经协商,某服装店给出的价格如下:
购买人数/人 | 1~50人 | 50~100人 | 100以上人 |
每套服装价格/元 | 50 | 45 | 40 |
例如:若购买人数为60人,则购买共需花费60×45=2700元.
(1)如果两个班都以班为单位分别购买,则一共需花费4875元,那么15,16班各有多少名学生?
(2)如果两个班联合起来,做为一个整体购买,则能节省多少元钱?
【题目】为了创建国家卫生城市,需要购买甲、乙两种类型的分类垃圾桶替换原来的垃圾桶,![]() ,
,![]() ,
,![]() 三个小区所购买的数量和总价如表所示.
三个小区所购买的数量和总价如表所示.
甲型垃圾桶数量(套) | 乙型垃圾桶数量(套) | 总价(元) | |
|
|
|
|
|
|
|
|
|
|
|
|
(1)问甲型垃圾桶、乙型垃圾桶的单价分别是每套多少元?
(2)求![]() ,
,![]() 的值.
的值.