题目内容
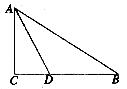
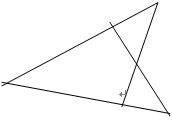
如图,(1)P是等腰三角形A BC底边BC上的一人动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R。请观察AR与AQ,它们有何关系?并证明你的猜想。
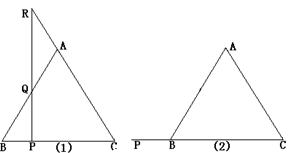
(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图15(2)中完成图 形,并给予证明。

(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图15(2)中完成图 形,并给予证明。
直角三角形的角度运算规律;AR=AQ
试题分析:解:(1)AR=AQ,理由如下:
∵AB=AC
∴∠B=∠C
∵RP⊥BC
∴∠B+∠BQP=∠C+∠PRC=90º
∴∠BQP=∠PRC
∵∠BQP=∠AQR
∴∠PRC=∠AQR
∴AR=AQ
(2)猜想仍然成立。证明如下:
∵AB=AC
∴∠ABC=∠C
∵∠ABC=∠PBQ
∴∠PBQ=∠C
∵RP⊥BC
∴∠PBQ+∠BQP=∠C+∠PRC=90º
∴∠BQP=∠PRC
∴AR=AQ
点评:本题属于对直角三角形的基本运算规律和角度变换知识点的考查和运用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

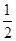 ∠B=
∠B=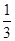 ∠C,那么△ABC是( )
∠C,那么△ABC是( )