题目内容
【题目】如图所示,在平面直角坐标系xoy中,直线y=![]() x+
x+![]() 交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l,将直线l绕点C按逆时针方向旋转,旋转角为α(0°<α<180°).
交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l,将直线l绕点C按逆时针方向旋转,旋转角为α(0°<α<180°).

(1)当直线l与直线y=![]() x+
x+![]() 平行时,求出直线l的解析式;
平行时,求出直线l的解析式;
(2)若直线l经过点A,①求线段AC的长;②直接写出旋转角α的度数;
(3)若直线l在旋转过程中与y轴交于D点,当△ABD、△ACD、△BCD均为等腰三角形时,直接写出符合条件的旋转角α的度数.
【答案】(1)y=![]() x
x![]() ;(2)①AC=2;②α=30°;(3)α=15°或60°或105°或150°
;(2)①AC=2;②α=30°;(3)α=15°或60°或105°或150°
【解析】
(1)设直线l的解析式为y=![]() x+b,把点C(1,0)代入求出b即可;
x+b,把点C(1,0)代入求出b即可;
(2)①求出点A的坐标,利用两点间距离公式即可求出AC的长;②如图1中,由CE∥OA,推出∠ACE=∠OAC,由tan∠OAC=![]() ,推出∠OAC=30°,即可解决问题;
,推出∠OAC=30°,即可解决问题;
(3)根据等腰三角形的判定和性质,分情况作出图形,进行求解即可.
解:(1)当直线l与直线y=![]() x+
x+![]() 平行时,设直线l的解析式为y=
平行时,设直线l的解析式为y=![]() x+b,
x+b,
∵直线l经过点C(1,0),
∴0=![]() +b,
+b,
∴b=![]() ,
,
∴直线l的解析式为y=![]() x
x![]() ;
;
(2)①对于直线y=![]() x+
x+![]() ,令x=0得y=
,令x=0得y=![]() ,令y=0得x=1,
,令y=0得x=1,
∴A(0,![]() ),B(1,0),
),B(1,0),
∵C(1,0),
∴AC=![]() ,
,
②如图1中,作CE∥OA,
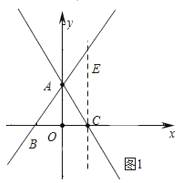
∴∠ACE=∠OAC,
∵tan∠OAC=![]() ,
,
∴∠OAC=30°,
∴∠ACE=30°,
∴α=30°;
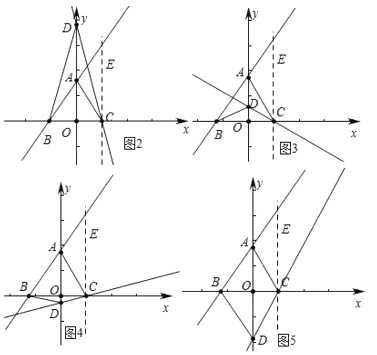
(3)①如图2中,当α=15°时,
∵CE∥span>OD,
∴∠ODC=15°,
∵∠OAC=30°,
∴∠ACD=∠ADC=15°,
∴AD=AC=AB,
∴△ADB,△ADC是等腰三角形,
∵OD垂直平分BC,
∴DB=DC,
∴△DBC是等腰三角形;
②当α=60°时,易知∠DAC=∠DCA=30°,
∴DA=DC=DB,
∴△ABD、△ACD、△BCD均为等腰三角形;
③当α=105°时,易知∠ABD=∠ADB=∠ADC=∠ACD=75°,∠DBC=∠DCB=15°,
∴△ABD、△ACD、△BCD均为等腰三角形;
④当α=150°时,易知△BDC是等边三角形,
∴AB=BD=DC=AC,
∴△ABD、△ACD、△BCD均为等腰三角形,
综上所述:当α=15°或60°或105°或150°时,△ABD、△ACD、△BCD均为等腰三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案