题目内容
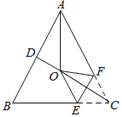
【题目】如图,在Δ![]() 中,已知
中,已知![]() 点
点![]() 为
为![]() 中点,点
中点,点![]() 在线段
在线段![]() 上以每秒
上以每秒![]() 的速度由
的速度由![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动。当点
点运动。当点![]() 的运动速度为每秒____
的运动速度为每秒____![]() 时,能够在某一时刻使得Δ
时,能够在某一时刻使得Δ![]() 与Δ
与Δ![]() 全等
全等

【答案】![]() 或
或![]() .
.
【解析】
设当△BPD与△CQP全等时,点Q的运动速度为每秒x个单位长度,时间为t,求出BD,求出∠B=∠C,根据全等三角形的判定得出两种情况,分别求出即可.
解:设当△BPD与△CQP全等时点Q的运动速度为每秒x个单位长度,时间为t,
∵AB=AC,
∴∠B=∠C,
∵AB=24,D为AB的中点,
∴BD=12,
若△BPD与△CQP全等,则有两种情况:
①BD=CP,BP=CQ,
即![]() ,
,
解得:![]() ;
;
②BD=CQ,BP=CP,
即12=xt,4t=16-4t,
解得:![]() ,
,![]() ,
,
∴当点![]() 的运动速度为每秒
的运动速度为每秒![]() 或
或![]() 时,使得三角形Δ
时,使得三角形Δ![]() 与Δ
与Δ![]() 全等.
全等.
故答案为:![]() 或
或![]() .
.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
【题目】已知二次函数y=ax2+bx(a≠0)中自变量x和函数值y的部分对应值如下表:
x | … | ﹣2.5 | ﹣2 | ﹣1 | 0 | 0.5 | … |
y | … | ﹣5 | 0 | 4 | 0 | ﹣5 | … |
(1)求二次函数解析式,并写出顶点坐标;
(2)在直角坐标系中画出该抛物线的图象;
(3)若该抛物线上两点A(x1,y1)、B(x2,y2)的横坐标满足x1<x2<﹣1,试比较y1与y2的大小,并说明理由.