Question

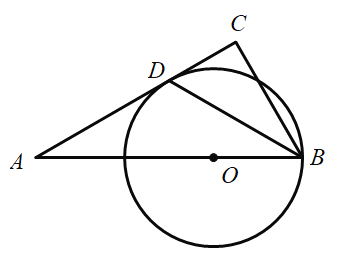
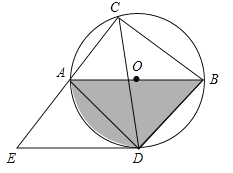
【题目】如图，⊙O的直径AB=10，弦AC=6，∠ACB的平分线交⊙O于D，过点D作DE∥AB交CA的延长线于点E，连接AD，BD．

（1）由AB，BD，围成的曲边三角形的面积是 ；

（2）求证：DE是⊙O的切线；

（3）求线段DE的长．

Answer 1

【答案】（1）；（2）证明见解析；（3）．

【解析】

（1）连接OD，由AB是直径知∠ACB=90°，结合CD平分∠ACB知∠ABD=∠ACD=45°，从而知∠AOD=90°，根据曲边三角形的面积=S扇形AOD+S△BOD可得答案；

（2）由∠AOD=90°，即OD⊥AB，根据DE∥AB可得OD⊥DE，即可得证；

（3）勾股定理求得BC=8，作AF⊥DE知四边形AODF是正方形，即可得DF=5，由∠EAF=90°﹣∠CAB=∠ABC知tan∠EAF=tan∠CBA，即，求得EF的长即可得．

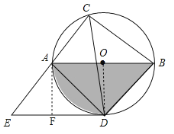
解：（1）如图，连接OD．∵AB是直径，且AB=10，

∴∠ACB=90°，AO=BO=DO=5．

∵CD平分∠ACB，∴∠ABD=∠ACD=∠ACB=45°，

∴∠AOD=90°，则曲边三角形的面积是

S扇形AOD+S△BOD=+×5×5=．

故答案为；

（2）由（1）知∠AOD=90°，即OD⊥AB．

∵DE∥AB，∴OD⊥DE，

∴DE是⊙O的切线；

（3）∵AB=10、AC=6，∴BC==8．

过点A作AF⊥DE于点F，则四边形AODF是正方形，∴AF=OD=FD=5，∴∠EAF=90°﹣∠CAB=∠ABC，

∴tan∠EAF=tan∠CBA，

∴，即，

∴EF=，

∴DE=DF+EF=+5=．