Question

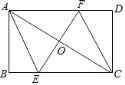
【题目】如图，在平行四边形ABCD中，过点B作BE∥AC，在BG上取点E，连接DE交AC的延长线于点F．

（1）求证：DF=EF；

（2）如果AD=2，∠ADC=60°，AC⊥DC于点C，AC=2CF，求BE的长．

Answer 1

【答案】（1）证明见解析；（2）2.

【解析】

（1）连接BD交AC于点O．由平行四边形的性质可知O为BD中点，又因为BG∥AF，进而证明DF=EF．

（2）利用直角三角形的性质和三角形中位线性质定理以及平行四边形的性质即可求出BE的长．

（1）证明：连接BD交AC于点O．

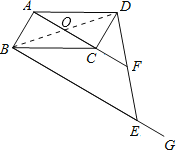
∵四边形ABCD是平行四边形，

∴OB=OD，

∵BG∥AF，

∴DF=EF．

（2）∵AC⊥DC，∠ADC=60°，AD=2，

∴AC=．

∵OF是△DBE的中位线，

∴BE=2OF．

∵OF=OC+CF，

∴BE=2OC+2CF．

∵四边形ABCD是平行四边形，

∴AC=2OC．

∵AC=2CF，

∴BE=2AC=2．