题目内容
【题目】已知,在 Rt△ABC中,∠ABC=90°, BD平分∠ ABC,∠CAD=45, AC=4,点E是线段BD的中点,则CE的最小值为 . 
【答案】![]() -1.
-1.
【解析】∵∠ABC=90°,
∴点A、B、C三点共圆,AC是直径,
又∵ BD平分∠ ABC,
∴∠DBC=45°,且∠CAD=45°,
∴点D也在点A、B、C三点所确定的圆上,
即点A、B、C、D四点共圆.
如下图:设此圆为圆O.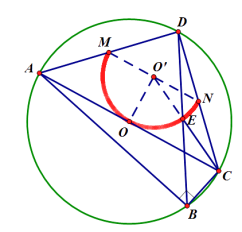
当点B与点A重合时,点E在AD的中点M处,点B与点C重合时,点E在DC的中点N处,
∴当点E的运动轨迹是以MN的中点O'为圆心,以O'O=O'M=O'N为半径的圆的一部分,
∴当点E运动到CE所在的直线过圆心O'时,CE有最小值,
此时:连接O'O,MN,O'E,
∵AC是直径, AC=4,且∠CAD=45°,M、N分别是AD、DC中点
∴![]() ADC是等腰直角三角形,O'O⊥AC,O'O=O'M=O'N=1,
ADC是等腰直角三角形,O'O⊥AC,O'O=O'M=O'N=1,
在Rt![]() O'OC中,O'C=
O'OC中,O'C=![]() =
=![]() ,
,
∴CE=O'C-O'N=![]() -1.
-1.
所以答案是:![]() -1.
-1.
【考点精析】通过灵活运用勾股定理的概念,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

练习册系列答案
相关题目