��Ŀ����
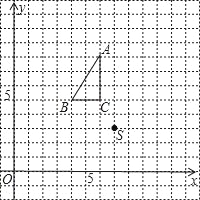
����Ŀ����ͼ��lA��lB�ֱ��ʾA������B�ﳵ��ͬһ·����ʻ��·��S��ʱ��t�Ĺ�ϵ��
��1��B����ʱ��A�������ǧ�ף�
��2��B����������Сʱ��A������
��3��B����һ��·�����г��������ϣ����� ���������õ�ʱ��������Сʱ��
��4����B�����г����������ϣ����ֳ���ʱ���ٶ�ǰ��������Сʱ��A��������������B�ij���������ǧ�ף���ͼ�б�ʾ�����������C��
��5�����A���ߵ�·��S��ʱ��t�ĺ�����ϵʽ����д�����̣�

���𰸡���1��10;��2��3;��3��1Сʱ;��4��������;��5��S=![]() x+10����
x+10����
��������
��1����ͼ�Ͽɿ���B����ʱ��A���10ǧ�ף�
��2����ͼ��3Сʱʱ������ͼ���ཻ������3Сʱʱ������
��3��������ʱ�����·�̲����ʱ����1.5��0.5=1Сʱ��
��4������������ʱ��B�����ߵ�·�̺�ʱ������������ϵ���躯��ʽΪy=kx������0.5��7.5���㣬�������ʽ���Ӷ����������ʱ�䣬�Ӷ����·�̣�
��5��S��t�ĺ�����ϵ��һ�κ������躯����ΪS=kx+t������0��10���ͣ�3��22.5�����Ӷ��������ϵʽ��
�⣺��1��B����ʱ��A���10ǧ�ף�
��2��3Сʱʱ������
��3���������г���ʱ��Ϊ��1.5��05=1Сʱ��
��4����B��ǰ�Ĺ�ϵʽΪy=kx������0.5��7.5���㣮
7.5=0.5k
k=15��
y=15x��
����ʱ��S=y
![]() x+10=15x
x+10=15x
x=![]() ��
��
y=![]() ��15=
��15=![]() ��
��
![]() Сʱʱ��������ʱB�ߵ�·����
Сʱʱ��������ʱB�ߵ�·����![]() ǧ�ף�
ǧ�ף�
��5���躯����ΪS=kx+t���ҹ���0��10���ͣ�3��22.5����
![]() ��
��
���![]() ��
��
��S=![]() x+10��
x+10��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�