��Ŀ����
����Ŀ����һ����װ�н���ˮ�ܵ�30��������ˮ�ܵ�λʱ���ڽ�����ˮ����һ���ģ����
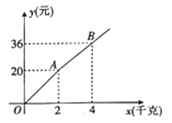
ijʱ�̿�ʼ��4������ֻ��ˮ����ˮ��������8�����ڼȽ�ˮ�ֳ�ˮ���õ�ˮ��y(��)
��ʱ��x(��)֮��ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ��������˵����

��ÿ���ӽ�ˮ5�����ڵ�4��x��12ʱ��������ˮ���ڼ��٣�
����12���Ӻ�ֻ��ˮ������ˮ����Ҫ8���ӿ���ˮ���ꣻ
������һ��ʼ����ˮ��ͬʱ����Ҫ24���ӿ��Խ�����������
����˵������ȷ����(����)
A. 1�� B. 2�� C. 3�� D. 4��
���𰸡�C
��������
����ͼ����Եõ�������ˮ��4����עˮ20������ͬʱ��ˮ�ܣ�8�����ڷŽ�10��ˮ���ݴ˼��ɽ��
�⣺��ÿ���ӽ�ˮ![]() =5������������ȷ��
=5������������ȷ��
�ڵ�4��x��12ʱ��y��x��������������������ˮ�������ӣ����������
��ÿ���ӷ�ˮ5-![]() =5-1.25=3.75����
=5-1.25=3.75����
�����ˮ��Ҫ![]() =8�����ӣ�����������ȷ��
=8�����ӣ�����������ȷ��
��ͬʱ��ˮ�ܺͷ�ˮ�ܣ�ÿ���ӽ�ˮ![]() =1.25������ͬʱ����Ҫ������������Ҫ��ʱ����
=1.25������ͬʱ����Ҫ������������Ҫ��ʱ����![]() =24�����ӣ���������ȷ��
=24�����ӣ���������ȷ��
��ѡ��C��

����Ŀ��ij��ҵ������һ��������Ŀ��Ϊ�˽�Լ��Դ����������������ҵ��������A��B�����ͺŵ���ˮ�����豸��8̨������������±���
A�� | B�� | |
�۸���Ԫ/̨�� | 12 | 10 |
����ˮ������������/�£� | 200 | 160 |
��Ԥ�㣬��ҵ���֧��89��Ԫ�����豸����Ҫ���´�����ˮ����������1380�֣�
��1������ҵ�м��ֹ�����
��2�����ַ�����ʡǮ��˵�����ɣ�