题目内容
【题目】如果一个三角形的两个内角α，β满足α+2β=90°，那么我们称这样的三角形为“非常三角形”．
（1）若△ABC是“非常三角形”，∠C＞90°，∠A=50°，则∠B= ．
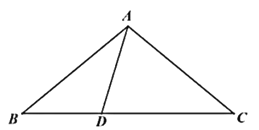
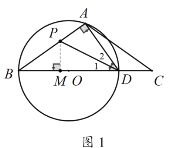
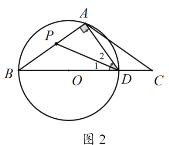
（2）如图，△ABC中，AB=AC，D是边BC上一点，以BD为直径的⊙O经过点A，连结AD．
①求证：△ADC为“非常三角形”．
②若sinB=
，AB=8，弦AB上是否存在一点P，使得△BDP是“非常三角形”，若存在，请求出线段AP的长度；若不存在，请说明理由．
【答案】（1）
；（2）①证明见解析；②
或3．
【解析】
（1）先根据三角形的内角和定理可得
，再根据“非常三角形”的定义即可得；
（2）①先根据圆周角定理可得
，从而可得
，再根据等腰三角形的性质可得
，然后根据三角形的外角性质、等量代换即可得证；
②先解直角三角形求出
，再根据三角形的外角性质求出
，据此分如图1和如图2（见解析）两种情况，然后分别利用相似三角形的判定与性质求解即可得．
（1）
则由“非常三角形”的定义得：
，即
解得
故答案为：；
（2）①∵BD是直径
∴
∴
∵
∴
∵
∴
∴
是“非常三角形”；
②在
中，
，
设
，则
由勾股定理得：
，解得
∴
因为
所以根据“非常三角形”的定义，分以下两种情况：
情况1：如图1，若
，
是“非常三角形”
∵
∴
过点P作
由角平分线的性质得：
在
和
中，
，即
解得
情况2：如图2，若
，是“非常三角形”
∵
∴
在
和中，
，即
解得
综上，线段AP的长度为或3．
练习册系列答案
相关题目
