Question

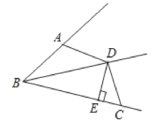
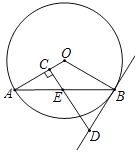
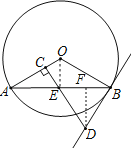
【题目】如图，AB是⊙O的弦，过AB的中点E作EC⊥OA，垂足为C，过点B作直线BD交CE的延长线于点D，使得DB=DE．

（1）求证：BD是⊙O的切线；

（2）若AB=12，DB=5，求△AOB的面积．

Answer 1

【答案】（1）证明见解析；（2）27．

【解析】（1）根据等腰三角形的性质和切线的判定方法可以求得∠OBD的度数，从而可以证明结论成立；

（2）要求△AOB的面积只要求出OE的长即可，根据题目中的条件和三角形相似的知识可以求得OE的长，从而可以解答本题．

（1）∵OA=OB，DB=DE，

∴∠A=∠OBA，∠DEB=∠DBE，

∵EC⊥OA，∠DEB=∠AEC，

∴∠A+∠DEB=90°，

∴∠OBA+∠DBE=90°，

∴∠OBD=90°，

∵OB是圆的半径，

∴BD是⊙O的切线；

（2）过点D作DF⊥AB于点F，连接OE，

∵点E是AB的中点，AB=12，

∴AE=EB=6，OE⊥AB，

又∵DE=DB，DF⊥BE，DB=5，DB=DE，

∴EF=BF=3，

∴DF==4，

∵∠AEC=∠DEF，

∴∠A=∠EDF，

∵OE⊥AB，DF⊥AB，

∴∠AEO=∠DFE=90°，

∴△AEO∽△DFE，

∴，

即，得EO=4.5，

∴△AOB的面积是：=27．