题目内容
【题目】如图,⊙O的半径为5,弦AB⊥CD于E,AB=CD=8.
(1)求证:AC=BD;
(2)若OF⊥CD于F,OG⊥AB于G,试说明四边形OFEG是正方形;
【答案】(1)证明见解析;(2)四边形OFEG是正方形,理由见解析.
【解析】
(1)根据圆心角、弧、弦的关系先由AB=CD判断![]() ,再得到
,再得到![]() ,从而判断AC=BD;
,从而判断AC=BD;
(2)先证明四边形OFEG为矩形,连结OA、OD,如图,再根据垂径定理得到CF=DF,AG=BG,则利用CD=AB得到AG=DF,然后根据正方形的判定方法可判断四边形OFEG是正方形;
(1)证明:∵AB=CD,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴AC=BD
(2)四边形OFEG是正方形
理由如下:
如图,连接OA、OD.
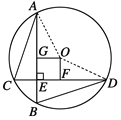
∵AB⊥CD,OF⊥CD,OG⊥AB,
∴四边形OFEG是矩形,DF=![]() CD,AG=
CD,AG=![]() AB.
AB.
∵AB=CD,
∴DF=AG.
∵OD=OA,
∴OD=OA,
∴△OFD≌△OGA,
∴OF=OG.
∴矩形OFEG是正方形

【题目】已知变量x、y对应关系如下表已知值呈现的对应规律.
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 1 | 2 | 3 | 4 | … |
y | … |
|
| 1 | 2 | ﹣2 | ﹣1 | ﹣ | ﹣ | … |
(1)依据表中给出的对应关系写出函数解析式,并在给出的坐标系中画出大致图象;
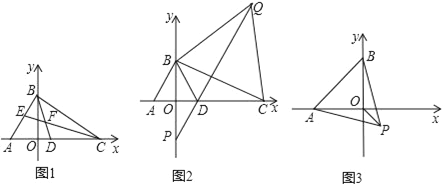
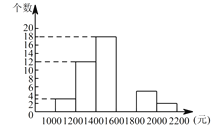
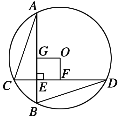
(2)在这个函数图象上有一点P(x,y)(x<0),过点P分别作x轴和y轴的垂线,并延长与直线y=x﹣2交于A、B两点,若△PAB的面积等于![]() ,求出P点坐标.
,求出P点坐标.
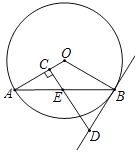
【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)求证:BD是⊙O的切线;
(2)若AB=12,DB=5,求△AOB的面积.
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为![]() 千克,烤制时间为
千克,烤制时间为![]() ,估计当
,估计当![]() 千克时,
千克时,![]() 的值为( )
的值为( )
A.138B.140C.148D.160