Question

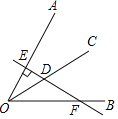
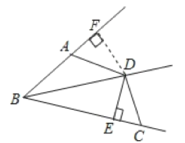
【题目】如图，已知BD为∠ABC的平分线，DE⊥BC于E，且AB+BC=2BE.

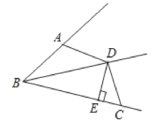
(1)求证：∠BAD+∠BCD=180°；

(2)若将条件“AB+BC=2BE”与结论“∠BAD+∠BCD=180°”互换，结论还成立吗?请说明理由。

Answer 1

【答案】（1）见解析；（2）结论仍然成立，理由见解析；

【解析】

（1）首先过D作DF⊥BA，垂足为F，再根据条件AB+BC=2BE可得AB+EC=BE，再证明Rt△BFD≌Rt△BED，可得FB=BE，即AB+AF=BE，进而得到AF=EC，然后再证明△AFD≌△CED可得∠DCE=∠FAD，再根据∠BAD+∠FAD=180°，可得∠BAD+∠BCD=180°；

（2）过D作DF⊥BA，垂足为F，首先证明∠DCE=∠FAD，再证明△AFD≌△CED，可得AF=EC，然后证明Rt△BFD≌Rt△BED可得FB=BE，再根据线段的和差关系可得AB+BC=2BE．

(1)证明：过D作DF⊥BA，垂足为F，

∵AB+BC=2BE，

∴AB=BE+BEBC，

AB=BE+BEBEEC，

AB=BEEC，

AB+EC=BE，

∵BD为∠ABC的平分线，DE⊥BC，DF⊥BA，

∴DF=DE，

在Rt△BFD和Rt△BED中 ，

∴Rt△BFD≌Rt△BED(HL)，

∴FB=BE，

∴AB+AF=BE，

又∵AB+EC=BE，

∴AF=EC，

在△AFD和△CED中 ，

∴△AFD≌△CED(SAS)，

∴∠DCE=∠FAD，

∵∠BAD+∠FAD=180°，

∴∠BAD+∠BCD=180°；

(2)可以互换，结论仍然成立，理由如下：

过D作DF⊥BA，垂足为F，

∵∠BAD+∠FAD=180°,∠BAD+∠BCD=180°，

∴∠DCE=∠FAD，

∵BD为∠ABC的平分线，DE⊥BC，DF⊥BA，

∴DF=DE，

在△AFD和△CED中 ，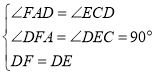

∴△AFD≌△CED(AAS)，

∴AF=EC，

在Rt△BFD和Rt△BED中 ，

∴Rt△BFD≌Rt△BED(HL)，

∴FB=BE，

∴AB+AF=BE，

AB=BEAF=BEEC=BE(BCBE)=BEBC+BE=2BEBC，

即：AB+BC=2BE.