题目内容
【题目】如图,一艘游轮在A处测得北偏东45°的方向上有一灯塔B.游轮以20![]() 海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:
海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
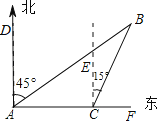
【答案】A处与灯塔B相距109海里.
【解析】直接过点C作CM⊥AB求出AM,CM的长,再利用锐角三角函数关系得出BM的长即可得出答案.
过点C作CM⊥AB,垂足为M,
在Rt△ACM中,∠MAC=90°﹣45°=45°,则∠MCA=45°,
∴AM=MC,
由勾股定理得:AM2+MC2=AC2=(20![]() ×2)2,
×2)2,
解得:AM=CM=40,
∵∠ECB=15°,
∴∠BCF=90°﹣15°=75°,
∴∠B=∠BCF﹣∠MAC=75°﹣45°=30°,
在Rt△BCM中,tanB=tan30°=![]() ,即
,即![]() ,
,
∴BM=40![]() ,
,
∴AB=AM+BM=40+40![]() ≈40+40×1.73≈109(海里),
≈40+40×1.73≈109(海里),
答:A处与灯塔B相距109海里.


练习册系列答案
相关题目
【题目】已知变量x、y对应关系如下表已知值呈现的对应规律.
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 1 | 2 | 3 | 4 | … |
y | … |
|
| 1 | 2 | ﹣2 | ﹣1 | ﹣ | ﹣ | … |
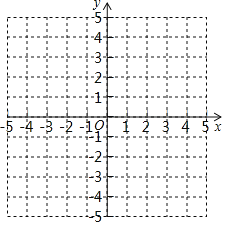
(1)依据表中给出的对应关系写出函数解析式,并在给出的坐标系中画出大致图象;
(2)在这个函数图象上有一点P(x,y)(x<0),过点P分别作x轴和y轴的垂线,并延长与直线y=x﹣2交于A、B两点,若△PAB的面积等于![]() ,求出P点坐标.
,求出P点坐标.