题目内容
【题目】如图,已知∠MON=30°,点A1、A2、A3……在射线ON上,点B1、B2、B3……在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4……均为等边三角形,且OA1=1.
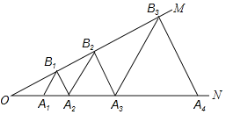
(1)分别求出△A1B1A2、△A3B3A4的边长;
(2)求△A7B7A8的周长(直接写出结果).
【答案】(1)1,4;(2)198.
【解析】
(1)根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4,可得结论;
(2)由(1)同理得:A4B4=8B1A2=8,A5B5=16B1A2…进而得出答案.
解:(1)如图,
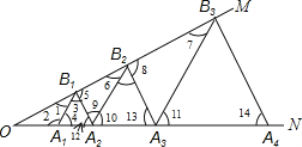
∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°-120°-30°=30°,
∴∠1=∠MON=30°,
∴A1B1=OA1=1,即△A1B1A2的边长为1;
又∵∠3=60°,
∴∠5=180°-60°-30°=90°,
∵A2B1=1,
∴A2B2=2A2B1=2,即△A2B2A3的边长为2;
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4,即△A3B3A4的边长为4;
综上,△A1B1A2的边长为1;△A3B3A4的边长为4;
(2)△A7B7A8的周长是198.
解:由(1)同理得:A4B4=8B1A2=8=23,
A5B5=16B1A2=16=24,
以此类推:A7B7=26=64;
∴△A7B7A8的周长=3×64=198.

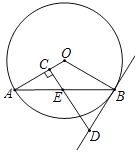
【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)求证:BD是⊙O的切线;
(2)若AB=12,DB=5,求△AOB的面积.
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为![]() 千克,烤制时间为
千克,烤制时间为![]() ,估计当
,估计当![]() 千克时,
千克时,![]() 的值为( )
的值为( )
A.138B.140C.148D.160