题目内容
如图,已知正方形ABCD的边长为8cm,点E、F分别在边BC、CD上,∠EAF=45°. 当EF=8cm时,△AEF的面积是 cm2; 当EF=7cm时,△EFC的面积是 cm2.

32,8
试题分析:延长EB至G,使BG=DF,连接AG.根据正方形的性质,证得△ABG≌△ADF,△FAE≌△GAE,即可求得△AEF的面积,从而求得△EFC的面积.
延长EB至G,使BG=DF,连接AG

∵正方形ABCD,
∴AB=AD,∠ABG=∠ADF=∠BAD=90°,
∵BG=DF,
∴△ABG≌△ADF,
∴AG=AF,∠BAG=∠DAF
∵∠EAF=45°
∴∠FAE=∠GAE=45°,
∵AE=AE,
∴△FAE≌△GAE,
∴EF=EG
当EF=8cm时,EF=EG=8cm
∴△AEF的面积=△GAE的面积=

当EF=7cm时,EF=EG=7cm
∴△EFC的面积=正方形ABCD的面积-2△AEF的面积=

点评:解答本题的关键是熟练掌握旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.

练习册系列答案
相关题目
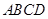 的边长为4cm,则图中阴影部分的面积为( )cm2.
的边长为4cm,则图中阴影部分的面积为( )cm2.
 处,且点
处,且点
 的顶点A、B、C在小正方形的顶点上.将
的顶点A、B、C在小正方形的顶点上.将 ,然后将△
,然后将△ 顺时针旋转90°得到△
顺时针旋转90°得到△ .
.
 在变换到点
在变换到点 的过程中经过的路线长;
的过程中经过的路线长; 在变换到线段
在变换到线段 的过程中扫过的图形的面积.
的过程中扫过的图形的面积.

