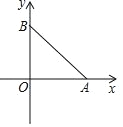Question

【题目】问题探究

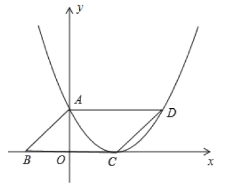
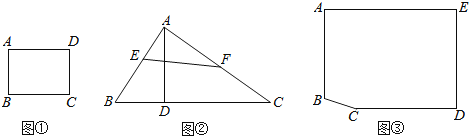
（1）如图①，在矩形ABCD中，AB=3，BC=4，如果BC边上存在点P，使△APD为等腰三角形，那么请画出满足条件的一个等腰三角形△APD，并求出此时BP的长；

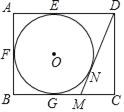
（2）如图②，在△ABC中，∠ABC=60°，BC=12，AD是BC边上的高，E、F分别为边AB、AC的中点，当AD=6时，BC边上存在一点Q，使∠EQF=90°，求此时BQ的长；

问题解决

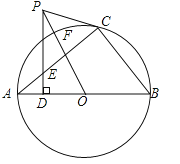
（3）有一山庄，它的平面图为如图③的五边形ABCDE，山庄保卫人员想在线段CD上选一点M安装监控装置，用来监视边AB，现只要使∠AMB大约为60°，就可以让监控装置的效果达到最佳，已知∠A=∠E=∠D=90°，AB=270m，AE=400m，ED=285m，CD=340m，问在线段CD上是否存在点M，使∠AMB=60°？若存在，请求出符合条件的DM的长，若不存在，请说明理由．

Answer 1

【答案】（1）2；4-；；（2）3+;（3）（400-45-30）米．

【解析】

（1）由于△PAD是等腰三角形，底边不定，需三种情况讨论，运用三角形全等、矩形的性质、勾股定理等知识即可解决问题．

（2）以EF为直径作⊙O，易证⊙O与BC相切，从而得到符合条件的点Q唯一，然后通过添加辅助线，借助于正方形、特殊角的三角函数值等知识即可求出BQ长．

（3）要满足∠AMB=60°，可构造以AB为边的等边三角形的外接圆，该圆与线段CD的交点就是满足条件的点，然后借助于等边三角形的性质、特殊角的三角函数值等知识，就可算出符合条件的DM长．

（1）①作AD的垂直平分线交BC于点P，如图①，

则PA=PD．

∴△PAD是等腰三角形．

∵四边形ABCD是矩形，

∴AB=DC，∠B=∠C=90°．

∵PA=PD，AB=DC，

∴Rt△ABP≌Rt△DCP（HL）．

∴BP=CP．

∵BC=4，

∴BP=CP=2．

②以点D为圆心，AD为半径画弧，交BC于点P′，如图①，

则DA=DP′．

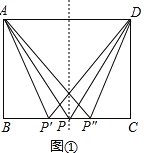
∴△P′AD是等腰三角形．

∵四边形ABCD是矩形，

∴AD=BC，AB=DC，∠C=90°．

∵AB=3，BC=4，

∴DC=3，DP′=4．

∴CP′==．

∴BP′=4-．

③点A为圆心，AD为半径画弧，交BC于点P″，如图①，

则AD=AP″．

∴△P″AD是等腰三角形．

同理可得：BP″=．

综上所述：在等腰三角形△ADP中，

若PA=PD，则BP=2；

若DP=DA，则BP=4-；

若AP=AD，则BP=．

（2）∵E、F分别为边AB、AC的中点，

∴EF∥BC，EF=BC．

∵BC=12，

∴EF=6．

以EF为直径作⊙O，过点O作OQ⊥BC，垂足为Q，连接EQ、FQ，如图②．

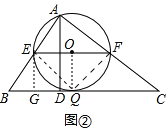
∵AD⊥BC，AD=6，

∴EF与BC之间的距离为3．

∴OQ=3

∴OQ=OE=3．

∴⊙O与BC相切，切点为Q．

∵EF为⊙O的直径，

∴∠EQF=90°．

过点E作EG⊥BC，垂足为G，如图②．

∵EG⊥BC，OQ⊥BC，

∴EG∥OQ．

∵EO∥GQ，EG∥OQ，∠EGQ=90°，OE=OQ，

∴四边形OEGQ是正方形．

∴GQ=EO=3，EG=OQ=3．

∵∠B=60°，∠EGB=90°，EG=3，

∴BG=．

∴BQ=GQ+BG=3+．

∴当∠EQF=90°时，BQ的长为3+．

（3）在线段CD上存在点M，使∠AMB=60°．

理由如下：

以AB为边，在AB的右侧作等边三角形ABG，

作GP⊥AB，垂足为P，作AK⊥BG，垂足为K．

设GP与AK交于点O，以点O为圆心，OA为半径作⊙O，

过点O作OH⊥CD，垂足为H，如图③．

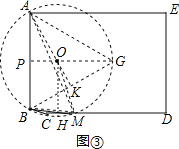
则⊙O是△ABG的外接圆，

∵△ABG是等边三角形，GP⊥AB，

∴AP=PB=AB．

∵AB=270，

∴AP=135．

∵ED=285，

∴OH=285-135=150．

∵△ABG是等边三角形，AK⊥BG，

∴∠BAK=∠GAK=30°．

∴OP=APtan30°

=135×

=45．

∴OA=2OP=90．

∴OH＜OA．

∴⊙O与CD相交，设交点为M，连接MA、MB，如图③．

∴∠AMB=∠AGB=60°，OM=OA=90．．

∵OH⊥CD，OH=150，OM=90，

∴HM==30．

∵AE=400，OP=45，

∴DH=400-45．

若点M在点H的左边，则DM=DH+HM=400-45+30img src="http://thumb.zyjl.cn/questionBank/Upload/2020/02/15/08/332c7e85/SYS202002150806083393103338_DA/SYS202002150806083393103338_DA.003.png" width="19" height="21" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />．

∵400-45+30＞340，

∴DM＞CD．

∴点M不在线段CD上，应舍去．

若点M在点H的右边，则DM=DH-HM=400-45-30．

∵400-45-30＜340，

∴DM＜CD．

∴点M在线段CD上．

综上所述：在线段CD上存在唯一的点M，使∠AMB=60°，

此时DM的长为（400-45-30）米．