��Ŀ����
����Ŀ����֪����ͼ�٣���ABC����AED������ȫ�ȵĵ���ֱ�������Σ��䶥��B��E�غϣ�����BAC=��AED=90�㣬OΪBC���е㣬FΪAD���е㣬����OF��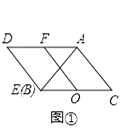
��1�����ⷢ��
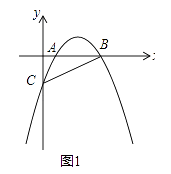
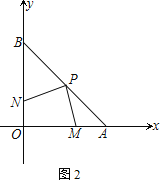
����ͼ�٣��߶�OF��EC��������ϵΪ��
�ڽ���AED�Ƶ�A��ʱ����ת45�㣬��ͼ�ڣ�OF��EC��������ϵΪ��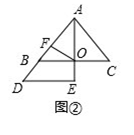
��2���������
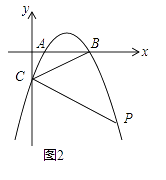
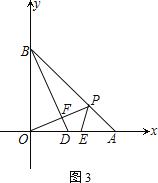
��ͼ���С�AED�Ƶ�A��ʱ����ת����ͼ����ʾ��λ�ã����ж��߶�OF��EC��������ϵ��������֤����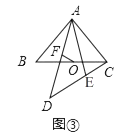
��3����չ̽��
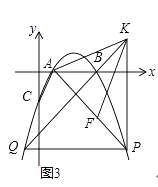
��ͼ���С�AED�Ƶ�A��ʱ����ת����ת��Ϊ����0��ܦ���90�㣬AD= ![]() ����AED����ת�����У����ڡ�ACDΪֱ�������Σ���ֱ��д���߶�CD�ij���
����AED����ת�����У����ڡ�ACDΪֱ�������Σ���ֱ��д���߶�CD�ij���
���𰸡�
��1��OF= ![]() EC��OF=
EC��OF= ![]() EC
EC
��2��
�⣺OF= ![]() EC��
EC��
֤�����ڵ���ֱ�ǡ�ADE�У�FΪAD���е㣬
��AF= ![]() AD=
AD= ![]() AE��
AE��
�ڵ���ֱ�ǡ�ABC�У�OΪBC���е㣬
��ͼ1��
����AO��
��AO= ![]() AC����BAO=��CAO=45�㣬
AC����BAO=��CAO=45�㣬
�ߡ�DAE=45�㣬
���DAE=��CAO��
���DAE����EAO=��CAO����EAO��
����DAO=��CAE��
��AE=AC��
��AF=AO��
�� ![]() =
= ![]() ��
��
���AFO�ס�AEC��
�� ![]() =
= ![]() =
= ![]() ��
��
��OF= ![]() EC��
EC��
��3��
�⣺�ߡ�ABC�͡�AED������ȫ�ȵĵ���ֱ�������Σ�
��AD=BC= ![]() ��
��
��ED=AE=AB=AC=1��
��ACDΪֱ��������ʱ�������������
�ٵ�AD��AB�غ�ʱ����ͼ2��
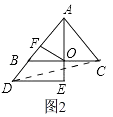
����CD��
�ߡ�ACDΪֱ�������Σ�AD��AC��
������ADE��ʱ����ת45�㣬
��AD= ![]() ��AC=1��
��AC=1��
���ɹ��ɶ����ɵ�CD= ![]() =
= ![]() ��
��
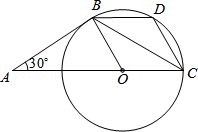
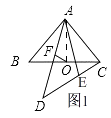
�ڵ�AE��AC�غ�ʱ����ͼ3��
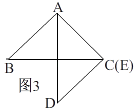
��ACDΪֱ�������Σ�AC��CD��
������ADE��ʱ����ת90�㣬��ʱCD=AC=1��
����CD�ij�Ϊ ![]() ��1��
��1��
���������⣺��1���١ߡ�ABC����AED������ȫ�ȵĵ���ֱ�������Σ�
��AD=BC��
��OΪBC���е㣬FΪAD���е㣬
��AF=OC��
�ߡ�BAC=��AED=90�㣬
��AD��BC��
���ı���AFOC��ƽ���ı��Σ�
��OF=AC= ![]() EC��
EC��
�ʴ𰸣�OF= ![]() EC������ͼ��
EC������ͼ��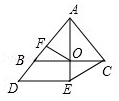
��AO= ![]() AC����BAO=��CAO=45�㣬
AC����BAO=��CAO=45�㣬
�ߡ�DAE=45�㣬
���DAE=��CAO��
���DAE����EAO=��CAO����EAO��
����DAO=��CAE��
��AE=AC��
��AF=AO��
�� ![]() =
= ![]() ��
��
���AFO�ס�AEC��
�� ![]() =
= ![]() =
= ![]() ��
��
��OF= ![]() EC��
EC��
�ʴ�OF= ![]() EC
EC
�����㾫����������Ĺؼ������������������ε�Ӧ�õ����֪ʶ�����ղ�ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�