题目内容
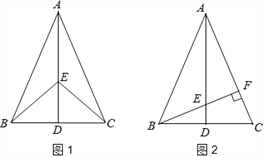
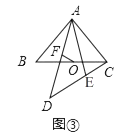
【题目】如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为 ![]() 的中点.
的中点. 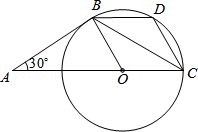
(1)求证:AB=BC;
(2)求证:四边形BOCD是菱形.
【答案】
(1)证明:∵AB是⊙O的切线,
∴OB⊥AB,
∵∠A=30°,
∴∠AOB=60°,
∵OB=OC,
∴∠OCB=∠OBC= ![]() ∠AOB=30°,
∠AOB=30°,
∴∠A=∠OCB,
∴AB=BC;
(2)证明:连接OD,
∵∠AOB=60°,
∴∠BOC=120°,
∵D为 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,∠BOD=∠COD=60°,
,∠BOD=∠COD=60°,
∵OB=OD=OC,
∴△BOD与△COD是等边三角形,
∴OB=BD=OC=CD,
∴四边形BOCD是菱形.
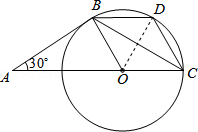
【解析】(1)由AB是⊙O的切线,∠A=30°,易求得∠OCB的度数,继而可得∠A=∠OCB=30°,又由等角对等边,证得AB=BC;(2)首先连接OD,易证得△BOD与△COD是等边三角形,可得OB=BD=OC=CD,即可证得四边形BOCD是菱形.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】小东根据学习函数的经验,对函数y= ![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)表格是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | ﹣ | 0 | | 1 | | 2 | | 3 | 4 | … |
y | … | |
| | 2 | | 4 | | 2 | |
| m | … |
表中m的值为;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数y= ![]() 的大致图象;
的大致图象;
(4)结合函数图象,请写出函数y= ![]() 的一条性质: .
的一条性质: .
(5)如果方程 ![]() =a有2个解,那么a的取值范围是 .
=a有2个解,那么a的取值范围是 .