Question

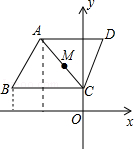
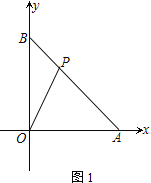
【题目】如图1，在平面直角坐标系中，A、B坐标为(6，0)、(0，6)，P为线段AB上的一点

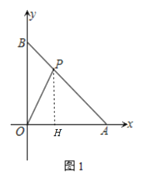
(1) 如图1，若S△AOP＝12，求P的坐标

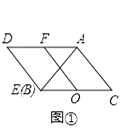
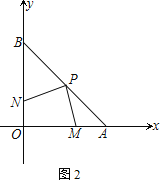
(2) 如图2，若P为AB的中点，点M、N分别是OA、OB边上的动点，点M从顶点A、点N从顶点O同时出发，且它们的速度都为1 cm/s，则在M、N运动的过程中，线段PM、PN之间有何关系？并证明

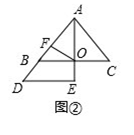
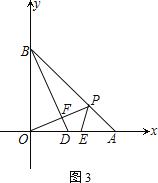
(3) 如图3，若P为线段AB上异于A、B的任意一点，过B点作BD⊥OP，交OP、OA分别与F、D两点，E为OA上一点，且∠PEA＝∠BDO，试判断线段OD与AE的数量关系，并说明理由

Answer 1

【答案】（1）P(2，4)；（2）PM＝PN，PM⊥PN，理由见解析；（3）OD＝AE，理由见解析

【解析】试题分析：（1）如图1中，作PH⊥OA于H．线求出直线AB的解析式，利用面积构建方程求出PH即可解决问题；

（2）结论：PM=PN，PM⊥PN．连接OP．只要证明△PON≌△PAM即可解决问题；

（3）结论：OD=AE．如图3中，作AG⊥x轴交OP的延长线于G．由△DBO≌△GOA，推出OD=AG，∠BDO=∠G，再证明△PAE≌△PAG即可解决问题；

试题解析：解：（1）如图1中，作PH⊥OA于H．

∵A（6，0），B（0，6），∴直线AB的解析式为y=﹣x+6．∵ OAPH=12，∴PH=4，当y=4时，4=﹣x+6，∴x=2，∴P（2，4）．

（2）结论：PM=PN，PM⊥PN．证明如下：

如图2中，连接OP．

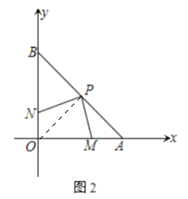
∵OB=OA，∠AOB=90°，PB=PA，∴OP=PB=PA，OP⊥AB，∠PON=∠A=45°，∴∠OPA=90°．

∵AM=ON，OP=OP，∴△PON≌△PAM，∴PN=PM，∠OPN=∠APM，∴∠NPM=∠OPA=90°，

∴PM⊥PN，PM=PN．

（3）结论：OD=AE．理由如下：

如图3中，作AG⊥x轴交OP的延长线于G．

∵BD⊥OP，∴∠OAG=∠BOD=∠OFD=90°，∴∠ODF+∠AOG=90°，∠ODF+∠OBD=90°，∴∠AOG=∠DBO，∵OB=OA，∴△DBO≌△GOA，∴OD=AG，∠BDO=∠G．∵∠BDO=∠PEA，∴∠G=∠AEP．∵∠PAE=∠PAG=45°，PA=PA，∴△PAE≌△PAG，∴AE=AG，∴OD=AE．