题目内容
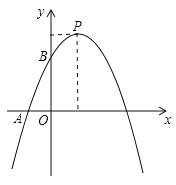
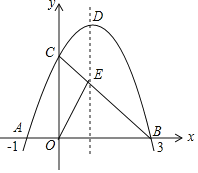
【题目】如图，已知抛物线y＝﹣x2+bx+c与x轴交于点A（﹣1，0）和点B（3，0），与y轴交于点C，连接BC交抛物线的对称轴于点E，D是抛物线的顶点．
（1）求此抛物线的解析式；
（2）直接写出点C和点D的坐标；
（3）若点P在第一象限内的抛物线上，且S△ABP＝4S△COE，求P点坐标；
（4）在平面内，是否存在点M使点A、B、C、M构成平行四边形，如果存在，直接写出M坐标；如果不存在，请说明理由．
【答案】（1）y＝﹣x2+2x+3；（2）C（0，3），D（1，4）；（3）P（2，3）；（4）存在，点M的坐标为（2，﹣3）或（4，3）或（﹣4，3）．
【解析】
（1）将A、B的坐标代入抛物线的解析式中，即可求出待定系数b、c的值，可求解；
（2）令x＝0，可得C点坐标，将函数解析式配方即得抛物线的顶点C的坐标；
（3）设P（x，y）（x＞0，y＞0），根据题意列出方程即可求得y，即得P点坐标；
（4）分三种情况讨论，利用平行四边形的性质及中点坐标公式可求解．
解：（1）∵抛物线y＝﹣x2+bx+c与x轴交于点A（﹣1，0）和点B（3，0），
∴
，
解得：
，
∴抛物线的解析式为y＝﹣x2+2x+3；
（2）令x＝0，则y＝3，
∴C（0，3），
∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，
∴D（1，4）；
（3）设P（x，y）（x＞0，y＞0），S△COE以OC为底，点E到y轴的距离为高，由（2）知，点E在对称轴x=1上，S△ABP以AB为底，点P到x轴的距离为高，
则S△COE＝
×1×3＝
，S△ABP＝×4y＝2y，
∵S△ABP＝4S△COE，
∴2y＝4×，
∴y＝3，
∴﹣x2+2x+3＝3，
解得：x1＝0（不合题意，舍去），x2＝2，
∴P（2，3）；
（4）存在，点M的坐标为（2，﹣3）或（4，3）或（﹣4，3）．
理由如下：
设点M（m，n），A（﹣1，0）、B（3，0），C（0，3），
若AB为对角线，AB的中点坐标和CM的中点坐标相同，
则
，
，
∴m＝2，n＝﹣3，
∴点M（2，﹣3）；
若BC为对角线，则
，
，
∴m＝4，n＝3，
∴点M（4，3）；
若AC为对角线，则
，
，
∴m＝﹣4，n＝3，
∴点M（﹣4，3）；
综上所述：点M的坐标为（2，﹣3）或（4，3）或（﹣4，3）．
