题目内容
【题目】在平面直角坐标系中,已知![]() ,
,![]() ,点
,点![]() ,
,![]() 在
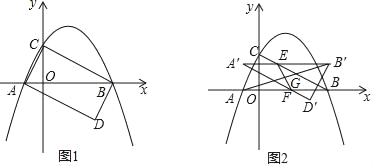
在![]() 轴上方,且四边形
轴上方,且四边形![]() 的面积为32,
的面积为32,
(1)若四边形![]() 是菱形,求点
是菱形,求点![]() 的坐标.
的坐标.
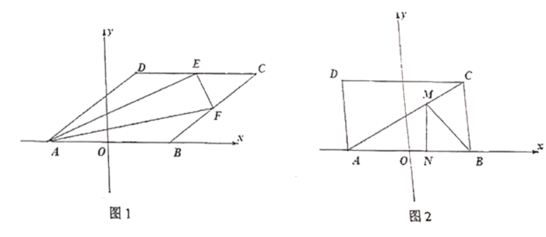
(2)若四边形![]() 是平行四边形,如图1,点
是平行四边形,如图1,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,且
的中点,且![]() ,求
,求![]() 的值.
的值.
(3)若四边形![]() 是矩形,如图2,点
是矩形,如图2,点![]() 为对角线
为对角线![]() 上的动点,
上的动点,![]() 为边
为边![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
【答案】(1)(![]() -4,4);(2)
-4,4);(2)![]() ;(3)
;(3)![]()
【解析】
(1)作DH⊥AB,先求出AB,根据菱形性质得AD=AB=8,再根据勾股定理求出AH,再求OH;
(2)延长EF与x轴相交于G,作EP⊥AB,根据平行线性质证△ECF≌△GBF(AAS),得BG=EC=4,EF=FG,AG=AB+BG=12,EG=2EF,根据勾股定理得:(AE+EG)2-2AEEG=AG2,根据三角形面积公式得:![]() 所以(AE+EG)2-2×48=122;
所以(AE+EG)2-2×48=122;
(3)作点B关于AC的对称点![]() ,作
,作![]() ,交AC于点M,此时BM+MN最小,连接
,交AC于点M,此时BM+MN最小,连接![]() ;根据矩形性质和轴对称性质得:AB=8,BC=
;根据矩形性质和轴对称性质得:AB=8,BC=![]() ,AC=
,AC=![]() ,求得
,求得![]() =
=![]() ,
,![]() =AB=8,
=AB=8,![]() ,设AN=x,则BN=8-x,由勾股定理可得:
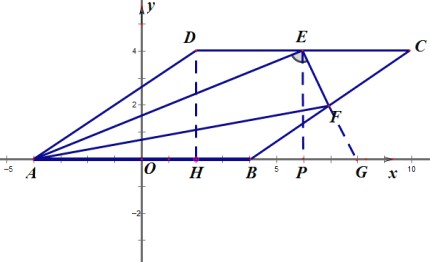
,设AN=x,则BN=8-x,由勾股定理可得: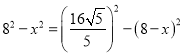 ,可进一步求出
,可进一步求出![]() .
.
(1)作DH⊥AB
因为![]() ,
,![]() ,
,
所以AB=4-(-4)=8,
因为四边形ABCD是菱形,
所以AD=AB=8,
因为四边形![]() 的面积为32,
的面积为32,
所以DH=32÷8=4
所以根据勾股定理可得:AH=![]()
所以OH=AH-OA=![]() -4
-4
所以点D的坐标是(![]() -4,4)
-4,4)
(2)延长EF与x轴相交于G,作EP⊥AB
因为四边形ABCD是平行四边形,
所以DC=AB=8,DC//AB
所以∠C=∠CBG,∠CEF=∠BGF,
因为E,F分别是CD,AB的中点,
所以DE=CE=4,CF=BF,
所以△ECF≌△GBF(AAS)
所以BG=EC=4,EF=FG
所以AG=AB+BG=12,EG=2EF,
又因为AF⊥EF
所以AE2+EG2=AG2
所以(AE+EG)2-2AEEG=AG2
由(1)知EP=DH=4
所以根据三角形面积公式得:![]()
所以![]()
所以(AE+EG)2-2×48=122
所以![]()
所以AE+2EF=![]()
(3)作点B关于AC的对称点![]() ,作
,作![]() ,交AC于点M,此时BM+MN最小;连接
,交AC于点M,此时BM+MN最小;连接![]() .
.
因为四边形ABCD是矩形,
所以由已知可得:AB=8,BC=![]()
所以AC=![]()
所以在三角形ABC中,AC上的高是:![]()
因为AC是![]() 的对称轴,
的对称轴,
所以![]() =
=![]() ,
,![]() =AB=8,
=AB=8,![]()
设AN=x,则BN=8-x,由勾股定理可得:
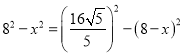
解得x=![]() ,
,
所以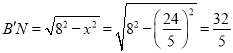
所以BM+MN=![]()
即BM+MN的最小值是![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案