Question

【题目】若点O是等腰△ABC的外心，且∠BOC＝60°，底边BC＝2，则△ABC的面积为(　　)

A. 2＋ B. C. 2＋或2－ D. 4＋2或2－

Answer 1

【答案】C

【解析】

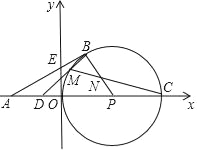
试题解析：由题意可得，如图所示，

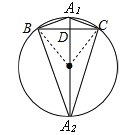
存在两种情况，当△ABC为△A1BC时，连接OB、OC，∵点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，OB=OC，∴△OBC为等边三角形，OB=OC=BC=2，OA1⊥BC于点D，∴CD=1，OD==，∴=BCA1D==；

当△ABC为△A2BC时，连接OB、OC，∵点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，OB=OC，∴△OBC为等边三角形，OB=OC=BC=2，OA1⊥BC于点D，∴CD=1，OD==，∴S△A2BC=BCA2D ==，由上可得，△ABC的面积为或，故选C．