Question

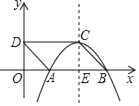
【题目】y=ax2+bx+c的图象与x轴交于A，B两点，与y轴交于点C，当△ABC为直角三角形时，则（　　）

A. ac=﹣1 B. ac=1 C. ac=±1 D. 无法确定

Answer 1

【答案】A

【解析】

设出A、B两点的坐标，根据根与系数的关系可得到AOBO，且OC=|c|，利用相似三角形的判定与性质可得到AO、BO、CO之间的关系，可得到ac的值．

设A（x1，0），B（x2，0），由△ABC为直角三角形可知x1、x2必异号，

∴x1x2=＜0，

由于函数图象与y轴相交于C点，所以C点坐标为（0，c），

∵∠ACO+∠BCO=90, ∠ACO+∠∠CAO=90,

∴∠BCO=∠CAO,

∴△ACO∽△CBO,

∴|OC|2=|AO||BO|，即c2=|x1||x2|=||，

故|ac|=1，ac=±1，

由于＜0，所以ac=﹣1．

故选：A．