��Ŀ����
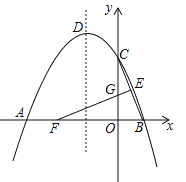
����Ŀ����ͼ��ֱ��y����x+5��x�ύ�ڵ�B����y�ύ�ڵ�D��������y����x2+bx+c��ֱ��y����x+5����B��D���㣬��C�������ߵĶ��㣮

��1���������ߵĽ���ʽ��
��2����M��ֱ��BD�Ϸ��������ϵ�һ�����㣬�������Ϊm������M��x��Ĵ��ߣ���ֱ��BD�ڵ�P�����߶�PM�ij������ʱ����m��ֵ��PM�����ֵ��
��3�������������Ƿ��������B��D�ĵ�Q��ʹ��BDQ��BD���ϵĸ�Ϊ3![]() �������������Q�����ꣻ����������˵�����ɣ�
�������������Q�����ꣻ����������˵�����ɣ�
���𰸡���1�������ߵı���ʽΪ��y����x2+4x+5����2����m��![]() ʱ��PM�����ֵ
ʱ��PM�����ֵ![]() ����3���������������ĵ�Q��������ΪQ1��2��9����Q2��3��8����Q3����1��0����Q4��6����7����
����3���������������ĵ�Q��������ΪQ1��2��9����Q2��3��8����Q3����1��0����Q4��6����7����
��������
��1��y=-x+5����x=0����y=5����y=0����x=5���ʵ�B��D������ֱ�Ϊ��5��0������0��5�������ô���ϵ����������⣻
��2��������ɵ�M������Ϊ��m����m2+4m+5��������P������Ϊ��m����m+5������ʾ��PM�ij��ȣ�PM=-m2+4m+5-��-m+5��=-m2+5m=-��m-![]() ��2+
��2+![]() �����ö��κ��������ʼ�����⣻
�����ö��κ��������ʼ�����⣻
��3����Q��QG��y�ύBD�ڵ�G����x���ڵ�E����QH��BD��H�����Q������Q��x����x2+4x+5������G��x����x+5������ʾ��QG�ij���QG=|-x2+4x+5-��-x+5��|=|-x2+5x|���������ɵá�BOD�ǵ���ֱ�������Σ�����֤�á�QHGΪ����ֱ�������Σ���BDQ��BD���ϵĸ�Ϊ3![]() ʱ����QH=HG=3
ʱ����QH=HG=3![]() ��QG=
��QG=![]() ��3
��3![]() =6��|-x2+5x|=6��������⣮
=6��|-x2+5x|=6��������⣮
�⣺��1��y����x+5����x��0����y��5����y��0����x��5��
�ʵ�B��D������ֱ�Ϊ��5��0������0��5����
����κ�������ʽΪ��y����x2+bx+5������B���������ʽ����ã�b��4��
�������ߵı���ʽΪ��y����x2+4x+5��
��2����M�������Ϊm��m��0������P��m����m+5����M��m����m2+4m+5����
��PM����m2+4m+5������m+5������m2+5m������m-![]() ��2+
��2+![]() ��
��
�൱m��![]() ʱ��PM�����ֵ
ʱ��PM�����ֵ![]() ��
��
��3����ͼ����Q��QG��y�ύBD�ڵ�G����x���ڵ�E����QH��BD��H��
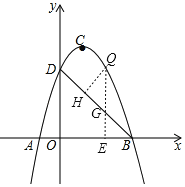
��Q��x����x2+4x+5������G��x����x+5����
��QG��|��x2+4x+5������x+5��|��|��x2+5x|��
�ߡ�BOD�ǵ���ֱ�������Σ�
���DBO��45����
���HGQ����BGE��45����
���QHG�ǵ���ֱ�������Σ�
����BDQ��BD���ϵĸ�Ϊ3![]() ʱ����QH��HG��3
ʱ����QH��HG��3![]() ��
��
��QG��![]() ��3
��3![]() ��6��
��6��
��|��x2+5x|��6��
����x2+5x��6ʱ�����x��2��x��3��
��Q��2��9����3��8����
����x2+5x����6ʱ�����x����1��x��6��
��Q����1��0����6����7����
���Ͽ�֪�������������ĵ�Q��������ΪQ1��2��9����Q2��3��8����Q3����1��0����Q4��6����7����

 һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�