题目内容
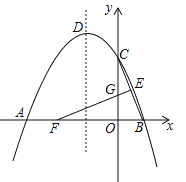
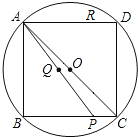
【题目】如图，
内接于⊙O，
，
是⊙O上与点
关于圆心
成中心对称的点，
是
边上一点，连结
．已知
，
，
是线段
上一动点，连结
并延长交四边形
的一边于点
，且满足
，则
的值为_______________．
【答案】1或
【解析】
解：因为
内接于圆，
，D是⊙O上与点B关于圆心O成中心对称的点，
∴AB=BC=CD=AD,
是正方形
①点R在线段AD上，
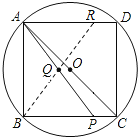
∵AD∥BC，
∴∠ARB=∠PBR，∠RAQ=∠APB，
∵AP=BR，
∴△BAP≌ABR，
∴AR=BP，
在△AQR与△PQB中，
，
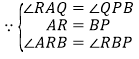②点R在线段CD上，此时△ABP≌△BCR，
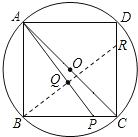
∴∠BAP=∠CBR．
∵∠CBR+∠ABR=90°，
∴∠BAP+∠ABR=90°，
∴BQ是直角△ABP斜边上的高，
∴QR=BR-BQ=5-2.4=2.6，
.
故答案为：1或.
练习册系列答案
相关题目
【题目】我们约定：体重在选定标准的
%（包含）范围之内时都称为“一般体重”．为了解某校七年级男生中具有“一般体重”的人数，我们从该校七年级男生中随机选出10名男生，测量出他们的体重（单位：kg），收集并整理得到如下统计表：
男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
体重 | 45 | 62 | 55 | 58 | 67 | 80 | 53 | 65 | 60 | 55 |
根据以上表格信息解决如下问题:
（1）将这组数据的三个统计量：平均数、中位数和众数填入下表：
平均数 | 中位数 | 众数 |
（2）请你选择其中一个统计量作为选定标准，说明选择的理由．并按此选定标准找出这10名男生中具有“一般体重”的男生．
