Question

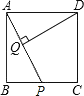
【题目】如图，AB是⊙O的直径，点C在⊙O上，CD与⊙O相切，AD∥BC，连接OD，AC．

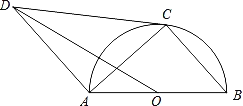
（1）求证：△ABC∽△DCA；

（2）若AC＝2，BC＝4，求DO的长．

Answer 1

【答案】（1）见解析；（2）3

【解析】

（1）连接OC，证明∠DCA=∠BCO，∠ABC=∠DCA，从而可判定△ABC∽△DCA；
（2）由△ABC∽△DCA可得

，求得DA，再由勾股定理先求得DC、AB，然后求得OD．

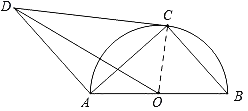
（1）证明：如图，连接OC，

∵CD与⊙O相切

∴∠OCD＝90°，

∴∠DCA+∠OCA＝90°，

∵AB为直径，

∴∠ACB＝90°，

∴∠ACO+∠BCO＝90°，

∴∠DCA＝∠BCO，

∵OC＝OB，

∴∠BCO＝∠CBO，

∴∠ABC＝∠DCA，

∴△ABC∽△DCA；

（2）∵△ABC∽△DCA，

∴＝，

∴＝，

∴DA＝5，

在Rt△ADC中，

DC＝＝＝3 ，

在Rt△ABC中，

AB＝＝6，

∴CO＝3，

在Rt△OCD中，

OD＝＝3，

∴DO的长为3．