题目内容
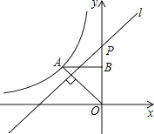
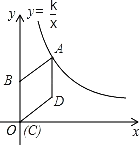
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=![]() (k>0,x>0)的图象上,点D的坐标为(4,3).若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=
(k>0,x>0)的图象上,点D的坐标为(4,3).若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=![]() (k>0,x>0)的图象上时,则菱形ABCD沿x轴正方向平移的距离( )
(k>0,x>0)的图象上时,则菱形ABCD沿x轴正方向平移的距离( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
过点D作x轴的垂线,垂足为F,首先得出A点坐标,再利用待定系数法求得反比例函数解析式为y=![]() ;将菱形ABCD沿x轴正方向平移,使得点D落在函数y=
;将菱形ABCD沿x轴正方向平移,使得点D落在函数y=![]() (x>0)的图象D′点处,得出点D′的纵坐标为3,求出其横坐标,进而得出菱形ABCD平移的距离.
(x>0)的图象D′点处,得出点D′的纵坐标为3,求出其横坐标,进而得出菱形ABCD平移的距离.
过点D作x轴的垂线,垂足为F,
∵点D的坐标为(4,3),
∴OF=4,DF=3,
∴OD=5,
∴AD=5,
∴点A坐标为(4,8),
∴k=xy=4×8=32,
∴反比例函数为y=![]() ,
,
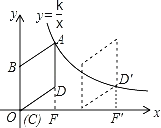
将菱形ABCD沿x轴正方向平移,使得点D落在函数y=![]() (x>0)的图象D′点处,
(x>0)的图象D′点处,
过点D′作x轴的垂线,垂足为F′.
∵DF=3,
∴D′F′=3,
∴点D′的纵坐标为3,
∵点D′在y=![]() (x>0)的图象上
(x>0)的图象上
∴3=![]() ,
,
解得:x=![]() ,
,
即OF′=![]() ,
,
∴FF′=![]() ﹣4=
﹣4=![]() ,
,
∴菱形ABCD平移的距离为![]() ,
,
故选:B.

练习册系列答案
相关题目