题目内容
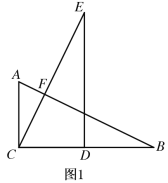
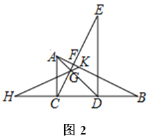
【题目】如图,在△ABC中,点D是线段AB的中点,DC⊥BC,作∠EAB=∠B,DE∥BC,连接CE.若![]() ,设△BCD的面积为S,则用S表示△ACE的面积正确的是( )
,设△BCD的面积为S,则用S表示△ACE的面积正确的是( )
A.![]() B.3S
B.3S
C.4SD.![]()
【答案】C
【解析】
延长AE,BC交于点F,易得AE=DE,由DE∥BC,D为AB的中点,可知DE为中位线,所以BF=2DE,设BC=2x,AE=DE=5x,则BF=10x,CF=BF-BC=8x,在△ABF和△ACF中,分别利用同高的两个三角形面积之比等于底边之比,可推出面积关系.
如图所示,延长AE,BC交于点F
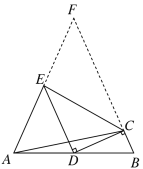
∵DE∥BC,∴∠ADE=∠B,
又∵∠EAB=∠B,∴∠ADE=∠EAB,∴AE=DE
∵D为AB的中点,DE∥BF,∴DE为△ABF的中位线,
∴BF=2DE,
设BC=2x,AE=DE=5x,则BF=10x,CF=BF-BC=8x,
在△ABC中,∵D是AB的中点,∴S△ACD=S△BCD=S
∴S△ABC=2S,
在△ABF中,![]()
∴![]()
在△ACF中,E为AF的中点,
∴![]()
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
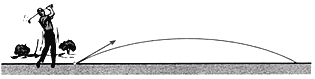
【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间(s)满足二次函数关系,t与h的几组对应值如下表所示:
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度.