题目内容
【题目】在等腰Rt△ABC中,AB=AC,∠BAC=90°
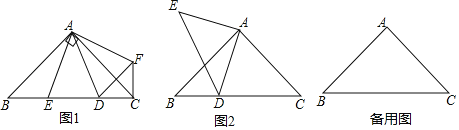
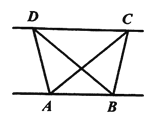
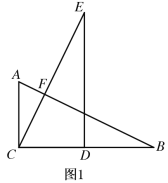
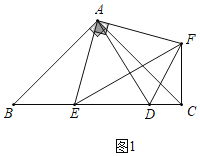
(1)如图1,D,E是等腰Rt△ABC斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF
①求证:△AED≌△AFD;
②当BE=3,CE=7时,求DE的长;
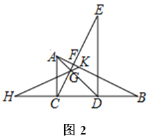
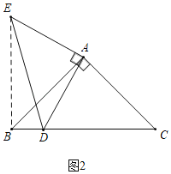
(2)如图2,点D是等腰Rt△ABC斜边BC所在直线上的一动点,连接AD,以点A为直角顶点作等腰Rt△ADE,当BD=3,BC=9时,求DE的长.
【答案】(1)①见解析;②DE=![]() ;(2)DE的值为3
;(2)DE的值为3![]() 或3
或3![]()
【解析】
(1)①先证明∠DAE=∠DAF,结合DA=DA,AE=AF,即可证明;②如图1中,设DE=x,则CD=7﹣x.在Rt△DCF中,由DF2=CD2+CF2,CF=BE=3,可得x2=(7﹣x)2+32,解方程即可;
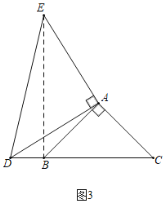
(2)分两种情形:①当点E在线段BC上时,如图2中,连接BE.由△EAD≌△ADC,推出∠ABE=∠C=∠ABC=45°,EB=CD=5,推出∠EBD=90°,推出DE2=BE2+BD2=62+32=45,即可解决问题;②当点D在CB的延长线上时,如图3中,同法可得DE2=153.
(1)①如图1中,
∵将△ABE绕点A逆时针旋转90°后,得到△AFC,
∴△BAE≌△CAF,
∴AE=AF,∠BAE=∠CAF,
∵∠BAC=90°,∠EAD=45°,
∴∠CAD+∠BAE=∠CAD+∠CAF=45°,
∴∠DAE=∠DAF,
∵DA=DA,AE=AF,
∴△AED≌△AFD(SAS);
②如图1中,设DE=x,则CD=7﹣x.
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵∠ABE=∠ACF=45°,
∴∠DCF=90°,
∵△AED≌△AFD(SAS),
∴DE=DF=x,
∵在Rt△DCF中, DF2=CD2+CF2,CF=BE=3,
∴x2=(7﹣x)2+32,
∴x=![]() ,
,
∴DE=![]() ;
;
(2)∵BD=3,BC=9,
∴分两种情况如下:
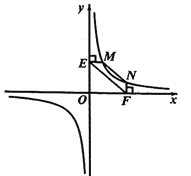
①当点E在线段BC上时,如图2中,连接BE.
∵∠BAC=∠EAD=90°,
∴∠EAB=∠DAC,
∵AE=AD,AB=AC,
∴△EAB≌△DAC(SAS),
∴∠ABE=∠C=∠ABC=45°,EB=CD=9-3=6,
∴∠EBD=90°,
∴DE2=BE2+BD2=62+32=45,
∴DE=3![]() ;
;
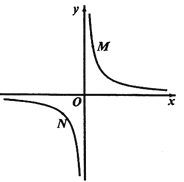
②当点D在CB的延长线上时,如图3中,连接BE.
同理可证△DBE是直角三角形,EB=CD=3+9=12,DB=3,
∴DE2=EB2+BD2=144+9=153,
∴DE=3![]() ,
,
综上所述,DE的值为3![]() 或3
或3![]() .
.

【题目】每天你是如何醒来的?某校有4000名学生,从不同班级不同层次抽取了400名学生进行调查,下表是这400名学生早晨起床方式的统计表:
起床方式 | 人数/人 |
别人叫醒 | 172 |
闹钟 | 88 |
自己醒来 | 64 |
其他 | 76 |
回答下列问题:
(1)该问题中总体是________;
(2)样本是__________;样本容量是__________.
(3)个体是________;
(4)估计全校学生中自己醒来的人数为________人.
【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间(s)满足二次函数关系,t与h的几组对应值如下表所示:
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度.