Question

【题目】已知：在△ABC中，AC=BC，点D在△ABC外部，且∠ACB+∠ADB=180°，连接AB、CD.

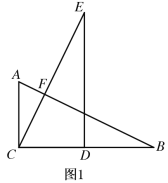
(1)如图1，当∠ACB=90°时，则∠ADC=______°.

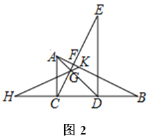
(2)如图2，当∠ACB=60°时，求证：DC平分∠ADB．

Answer 1

【答案】（1）45°；（2）证明见解析.

【解析】

（1）延长AD和CB，相交于点E，如图1，先判断△ABC为等腰直角三角形得到∠ABC=45°，再利用等角的余角可得∠BDE=∠ACB，则可判断△EBD∽△EAC，所以ED：EC=EB：EA，则ED：EB=EC：EA，加上∠DEC=∠BEA，则可判断△EDC∽△EBA，所以∠2=∠1，然后利用三角形内角和定理可得∠ADC=∠ABC=45°；

（2）延长AD和CB，相交于点E，如图2，先判断△ABC为等边三角形得到∠ABC=60°，与（1）一样可证明∠2=∠1，则∠ADC=∠ABC=60°，再计算出∠BDC=60°，于是可判断DC平分∠ADB．

（1）延长AD和CB，相交于点E，如图1，∵AC=BC，∠ACB=90°，

∴△ABC为等腰直角三角形，

∴∠ABC=45°，

∵∠ACB+∠ADB=180°，

而∠BDE+∠ADB=180°，∴∠BDE=∠ACB，

而∠BED=∠AEC，∴△EBD∽△EAC，

∴ED：EC=EB：EA，

∴ED：EB=EC：EA，

而∠DEC=∠BEA，∴△EDC∽△EBA，

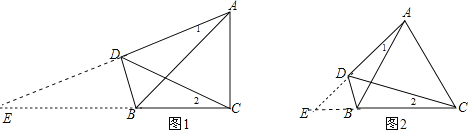
∴∠2=∠1，

∴∠ADC=∠ABC=45°，

（2）证明：延长AD和CB，相交于点E，如图2，

∵AC=BC，∠ACB=60°，

∴△ABC为等边三角形，

∴∠ABC=60°，

与（1）一样可证明△EDC∽△EBA，

∴∠2=∠1，

∴∠ADC=∠ABC=60°，

而∠ADB=180°-∠ACB=60°=120°，

∴∠BDC=60°，

∴DC平分∠ADB．