题目内容
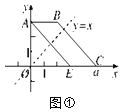
【题目】如图①,在平面直角坐标系xOy中,已知点A(0,3),B(2,3),OC=a.将梯形ABCO沿直线y=x折叠,点A落在线段OC上,对应点为E.
(1)求点E的坐标;
(2)①若BC∥AE,求a的值;(提示:两边互相平行的四边形是平行四边形,平行四边形的对边相等)
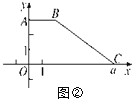
②如图②,若梯形ABCO的面积为2a,且直线y=mx将此梯形面积分为1∶2的两部分,求直线y=mx的函数表达式.
【答案】(1)点E的坐标为(3,0);(2) a=5;(3) y=![]() x或y=
x或y=![]() x.
x.
【解析】
(1)由折叠的性质可知OE=OA,由OA的长即可确定出点E的坐标;
(2)①由平行四边形的性质可知EC=AB,结合OE的长即可求得a的值;
②根据梯形的面积公式以及梯形的面积可求得a的值,从而可求得梯形的面积,设直线y=mx交BC于点D,点D的坐标为(xD,yD),由直线y=mx将梯形面积分为1∶2两部分,可得S△OCD=4或S△OCD=8,然后根据三角形的面积公式求得yD=![]() 或yD=
或yD=![]() ,利用待定系数法可得直线BC的函数表达式,将yD分别代入即可求得直线y=mx的解析式.
,利用待定系数法可得直线BC的函数表达式,将yD分别代入即可求得直线y=mx的解析式.
(1)由折叠的性质可知OE=OA,
∵A(0,3),∴OA=3,
∴OE=3,
∴点E的坐标为(3,0);
(2)∵BC∥AE,AB∥CE,∴四边形ABCE是平行四边形,
∴CE=AB=2,∴OC=OE+CE=5,
∴a=5;
(3)S梯形ABCO=![]() (AB+OC)·AO=2a,即
(AB+OC)·AO=2a,即![]() ,解得a=6,
,解得a=6,
∴S梯形ABCO=12,
设直线y=mx交BC于点D,点D的坐标为(xD,yD),
∵直线y=mx将梯形面积分为1∶2两部分,
∴S△OCD=![]() ×12=4或S△OCD=
×12=4或S△OCD=![]() ×12=8,
×12=8,
当S△OCD=4时,![]() ×6yD=4,解得yD=
×6yD=4,解得yD=![]() ,
,
当S△OCD=8时,![]() ×6yD=8,解得yD=
×6yD=8,解得yD=![]() ,
,
由B(2,3),C(6,0),可得直线BC的函数表达式为y=-![]() x+
x+![]() ,
,
则当yD=![]() 时,xD=
时,xD=![]() ,此时y=
,此时y=![]() x;
x;
当yD=![]() 时,xD=
时,xD=![]() ,此时y=
,此时y=![]() x,
x,
综上可知y=![]() x或y=
x或y=![]() x.
x.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案