题目内容
在△ABD中,E、H分别是AB、AD的中点,
则EH∥BD,
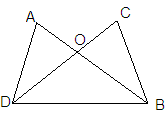
同理GH∥AC,如图,梯形ABCD中,AD//BC,AB=CD,对角线AC、BD交于点O,AC BD,E、F、G、H分别为AB、BC、CD、DA的中点.
BD,E、F、G、H分别为AB、BC、CD、DA的中点.

(1)求证:四边形EFGH为正方形;
(2)若AD=4,BC=6,求四边形EFGH的面积.
则EH∥BD,
同理GH∥AC,如图,梯形ABCD中,AD//BC,AB=CD,对角线AC、BD交于点O,AC
 BD,E、F、G、H分别为AB、BC、CD、DA的中点.
BD,E、F、G、H分别为AB、BC、CD、DA的中点.
(1)求证:四边形EFGH为正方形;
(2)若AD=4,BC=6,求四边形EFGH的面积.
(1)见解析;(2)12.5
试题分析:(1)先由三角形的中位线定理求出四边相等,然后由AC⊥BD入手,进行正方形的判断.
(2)连接EG,利用梯形的中位线定理求出EG的长,然后结合(1)的结论求出,也即得出了正方形EHGF的面积.
(1)在△ABC中,E、F分别是AB、BC的中点,
则
 ,同理
,同理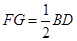 ,
,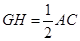 ,
, ,
,在梯形ABCD中,AB=DC,
故AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
设AC与EH交于点M,
又∵AC⊥BD,
∴EH⊥HG,
∴四边形EFGH是正方形.
(2)连接EG.
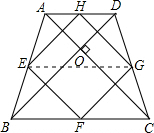
在梯形ABCD中,
∵E、G分别是AB、DC的中点,
∴EG=
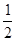 (AD+BC)=5,
(AD+BC)=5,在Rt△EHG中,
∵
 ,EH=GH,
,EH=GH,∴
 ,即四边形EFGH的面积为12.5.
,即四边形EFGH的面积为12.5.点评:解答本题的关键是根据三角形的内角和定理得出EH=HG=GF=FE,这是本题的突破口.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
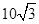 cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是 cm.
cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是 cm.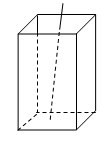
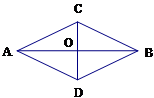
 ,M、N分别是AC、BD的中点,猜一猜MN与BD的位置关系,并说明结论。
,M、N分别是AC、BD的中点,猜一猜MN与BD的位置关系,并说明结论。
